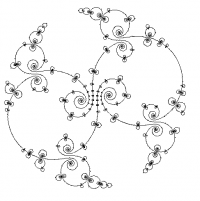
Ensemble limite

Exemple d'ensemble limite, par McMullen

L'ensemble limite d'un groupe Kleinien $\Gamma$ est noté $\Lambda(\Gamma)$ et possède plusieurs définitions équivalentes:

• C'est le complémentaire de l'ensemble de discontinuité $\Omega(\Gamma)$
• $\Omega(\Gamma)$ est l'ensemble sur lequel l'action est proprement discontinue
• $\Omega(\Gamma)$ est le plus grand ouvert sur lequel l'action est proprement discontinue
• $\Omega(\Gamma)$ est l'ensemble des points qui ont un voisinage sur lequel le groupe forme une famille normale
• $\Omega(\Gamma)$ est le plus grand ouvert sur lequel le groupe forme une famille normale
• $\Lambda(\Gamma)$ est l'ensemble d'accumulation de toute orbite
• $\Lambda(\Gamma)$ est l'adhérence de l'ensemble des points fixes des éléments $\neq\mathrm{id}$.

Si $\Gamma$ n'est pas un groupe fini, alors $\Lambda(\Gamma)$ est non-vide (et réciproquement).

Par contre, il arrive que $\Omega(\Gamma)$ soit vide, même pour des groupes de type fini.

Si $\Lambda(\Gamma)$ est fini alors il possède $0$, $1$ ou $2$ points et est d'une forme spécifique (c'est un sous-groupe d'un groupe à un paramètre) et est qualifié de groupe élémentaire. Sinon il c'est un compact parfait (sans point isolé) donc indénombrable.

Si $\Omega(\Gamma)\neq\emptyset$ alors $\Lambda(\Gamma)$ est d'intérieur vide.