Transformation d'une serie temporelle

1. Transformation d'une série temporelle en utilisant la procedure Expand. Soit une série de test

    
      1990  6 129.9 
      1990  7 130.4 
      1990  8 131.6 
      1990  9 132.7 
      1990 10 133.5 
      1990 11 133.8 
      1990 12 133.8 
      1991  1 134.6 
      1991  2 134.8 
      1991  3 135.0 
      1991  4 135.2 
      1991  5 135.6 
      1991  6 136.0 
      1991  7 136.2 
      ;
   

   Calculer et tracer $BX(t)$, $B^2X(t)$, $FX(t)$, $F^2X(t)$, $\mbox{CMA}(3)X(t)$(Moyenne mobile centrée), $\log X(t)$.

   Corrigé

    
   proc expand data=test out=out method=none; 
       id date; 
       convert x = x_lag2   / transformout=(lag 2); 
       convert x = x_lag1   / transformout=(lag 1); 
       convert x; 
       convert x = x_lead1  / transformout=(lead 1); 
       convert x = x_lead2  / transformout=(lead 2); 
       convert x = x_cmovave / transformout=(cmovave 3); 
       convert x = x_log / transformout=(log); 
   run; 
       
   title "Transformed Series"; 
      proc print data=out; 
   run;
      
   proc gplot data=out;
      plot(x_lag1, x_lead1, x_movave, x_log)
   run;
   quit;
   

   memo : il existe biensur beaucoup de option possibles (voir http://support.sas.com/onlinedoc/913/docMainpage.jsp)

   Corrigé

    
   + number	adds the specified number: x+number
   - number	subtracts the specified number: x-number
   * number	multiplies by the specified number: x*number
   & number	divides by the specified number: x & number
   

2. Simulation d'une série temporelle deterministe
   1. Créer une série temporelle hypothétique définit pour $t\in \{1,2,\cdots,12*10\}$.
      
      $$\displaystyle x_t = \sin\left (\frac{2\pi}{1\times 12}t\righ... ...displaystyle y_t = x_t+5\sin\left (\frac{2\pi}{3.3}t\right )$$
      
      

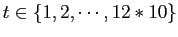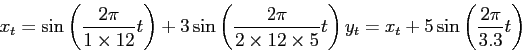
      Corrigé

       
      data serie;
        do t=1 to 10*12;
          x=sin(t*(2*3.14)/24)+sin(t*(2*3.14)/(24*5))*3;
          y=x+sin(t*(2*3.14)/3.3)*5;
          output;
        end;
      run;		
      
      /* juste pour etre jolie...*/
      symbol1 interpol=join color=black value=none;
      symbol2 interpol=join color=red value=none;
      symbol3 interpol=join color=green value=none;
      symbol4 interpol=join color=blue value=none;
      symbol5 interpol=join color=orange value=none;
      symbol6 interpol=join color=pink value=none;
      

   2. tracer ces deux series de facon superposée.

      Corrigé

       
      proc gplot data=serie;
        plot x*t y*t / overlay;
      run;
      quit; /* quitter la procedure data */