Finite element computations in Montjoie
Computation of finite element matrix
The general variational formulation for continuous elements is equal to (see the section devoted to the description of equations if you want more details about that formulation)

The tensors A, B, C, D and E are provided by the class defining the solved equation. These tensors will be of the form :
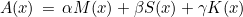
where

The variational formulation leads to the following linear system
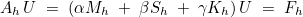
where the finite element matrix Ah is equal to
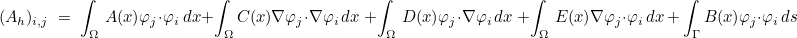
The matrices Mh, Sh and Kh are respectively the mass matrix, damping matrix and stiffness matrix. The finite element matrix is computed by calling method AddMatrixWithBC :
// The definition of the problem is constructed via EllipticProblem class
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE"); // name of the equation, it can be used to use an equivalent formulation of the same equation
ReadInputFile(input_file, var); // parameters of the ini file are read
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO"); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Real_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// but you can change them
Real_wp alpha = 2.0, beta = 0.5, gamma = 0.25;
nat_mat.SetCoefMass(alpha);
nat_mat.SetCoefDamping(beta);
nat_mat.SetCoefStiffness(gamma);
// matrix is added, so you need to clear it if you do not want to keep
// previous non-zero entries
A.Clear();
var.AddMatrixWithBC(A, nat_mat);
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Real_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
delete Ah;
The method AddMatrixWithBC calls method AddBoundaryConditionsTerms for terms due to boundary conditions and other extra terms then, the method AddMatrixFEM is called. In this last method, the boundary integrals (appearing only in discontinuous Galerkin formulation) are added to the matrix by the function AddElementaryFluxesDG, then the volume integrals are added by the function AssembleMatrix (which calls the function ComputeElementaryMatrix for each element of the mesh).
Functions related to computation of finite element matrix
| AssembleMatrix | assembles elementary matrices in order to form the finite element matrix |
| ComputeElementaryMatrix | computes elementary matrix for continuous or discontinuous elements |
| AddElementaryFluxesDG | adds boundary integrals that appear in DG formulation to a given matrix |
Public attributes of class VarProblem_Base
The class VarProblem_Base is the base class for steady (or time-harmonic) problems (class EllipticProblem). This class is abstract and non-template. It does not depend on the dimension or the type of equation. Below, we detail the public attributes of this class. Methods are listed in the next table.
| print_level | verbosity level |
| nb_unknowns_scal | number of scalar unknowns |
| nb_unknowns_vec | number of vectorial unknowns |
| nb_unknowns | number of unknowns |
| nb_components_en | number of components for the trace of the solution |
| nb_components_hn | number of components for the trace of the gradient of solution |
| nb_unknowns_hdg | number of surface unknowns (for HDG formulation) |
| type_element | type of the finite element used for the main unknown |
| other_type_element | type of the finite elements used for other unknowns |
| finite_element_name | name of the finite element used for the main unknown |
| name_other_elements | name of the finite elements used for other unknowns |
| mesh_num_unknown | list of mesh numberings to use for each unknown |
| offset_dof_unknown | incremental number of degrees of freedom for each unknown |
| offset_dof_condensed | incremental number of degrees of freedom for each unknown (after static condensation) |
| dg_formulation | Formulation used (continuous, discontinous or HDG) |
| sipg_formulation | true for Interior Penalty Discontinuous Galerkin |
| compute_dfjm1 | true if the jacobian matrices DFi need to be computed and stored |
| alpha_penalization | penalty parameter for discontinuous Galerkin formulations |
| delta_penalization | penalty parameter for discontinuous Galerkin formulations |
| upwind_fluxes | true if upwind fluxes will be used for a discontinuous Galerkin formulation |
| automatic_choice_penalization | true if penalty parameters are set automatically |
| Glob_CoefPenalDG | Penalty parameters for each face (IPDG) |
| mesh_data | Parameters for constructing the mesh |
| exit_if_no_boundary_condition | if true, the simulation is stopped if there is a boundary face without boundary condition |
| var_chrono | Object used to compute timings |
Methods of class VarProblem_Base
| GetNbDof | returns the number of degrees of freedom for the considered problem (i.e. size of the matrix) |
| SetNbDof | sets the number of degrees of freedom for the considered problem (i.e. size of the matrix) |
| GetNbMeshDof | returns the number of degrees of freedom for a mesh numbering |
| GetNbMeshNumberings | returns the number of mesh numberings |
| GetMeshNumberingBase | gives access to the mesh numbering |
| GetOffsetDofUnknown | returns the cumulative number of degrees of freedom for a given unknown |
| GetOffsetDofCondensed | returns the cumulative number of degrees of freedom for a given unknown (with static condensation) |
| GetDefaultOrder | returns the default order to use for the mesh geometry |
| FormulationDG | returns true if the problem is solved with a discontinuous Galerkin formulation |
| ComputeDFjm1 | returns true if the jacobian matrices DFi must be stored for the computation of the finite element matrix |
| FirstOrderFormulation | returns true if a mixed formulation is used (such that only first-order derivatives appear) |
| FirstOrderFormulationDG | returns true if the problem is a formulation involving only first-order derivatives in time and space |
| SetFirstOrderFormulation | informs that the problem is a formulation involving only first-order derivatives in time and space |
| UseExactIntegrationElement | returns true if exact integration will be used |
| GetOverIntegration | returns the additional degree to use in order to over-integrate |
| GetXmin | returns the minimum of x-coordinates of the physical domain (without PML) |
| GetYmin | returns the minimum of y-coordinates of the physical domain (without PML) |
| GetZmin | returns the minimum of z-coordinates of the physical domain (without PML) |
| GetXmax | returns the maximum of x-coordinates of the physical domain (without PML) |
| GetYmax | returns the maximum of y-coordinates of the physical domain (without PML) |
| GetZmax | returns the maximum of z-coordinates of the physical domain (without PML) |
| SetComputationalDomain | sets the extremities of the physical domain (without PML) |
| GetSquareOmega | returns the square of the pulsation |
| GetOmega | returns the pulsation |
| GetMiomega | returns -i ω for complex numbers, 1 for real numbers |
| GetMomega2 | returns -ω2 for complex numbers, 1 for real numbers |
| GetFrequency | returns the frequency |
| SetOmega | sets the pulsation |
| SetFrequency | sets the frequency |
| GetWaveLengthAdim | returns the characteristical length used for adimensionalization |
| GetDimension | returns the dimension (2 or 3) |
| GetNbComponentsUnknown | returns the number of components for an unknown (1, 2 or 3) |
| GetNbComponentsGradient | returns the number of components for the gradient of an unknown (1, 2 or 3) |
| GetNbLocalDof | returns the number of degrees of freedom for an element of the mesh |
| GetNbSurfaceDof | returns the number of degrees of freedom for a surfacic element of the mesh |
| GetNbDofBoundaries | returns the number of degrees of freedom associated with the boundary of an element |
| GetNbPointsQuadratureInside | returns the number of quadrature points inside an element of the mesh |
| WeightsND | returns the array containing quadrature weights for a given element of the mesh |
| ElementInsidePML | returns true if the i-th element belongs to PMLs |
| GetReferenceElementBase | returns the finite element associated with an element |
| GetSurfaceElementBase | returns the finite element associated with a surfacic element |
| WriteMesh | writes the mesh on a file |
| SetSameNumberPeriodicDofs | Periodic condition is enforced by using the same dof numbers |
| InitIndices | inits the number of references for physical indexes |
| GetNbPhysicalIndices | returns the number of references for physical indexes |
| SetIndices | sets physical indexes with parameters |
| SetPhysicalIndex | sets a single physical index with parameters |
| IsVaryingMedia | returns true if the i-th media is a media with variable physical coefficients |
| GetCoefficientPenaltyStiffness | returns the penalty coefficient for a given reference |
| GetPhysicalIndexName | returns the name of the m-th physical index |
| GetVelocityOnElements | computes the speed of propagation for each element |
| GetVelocityOfMedia | returns the speed of propagation for a given reference |
| GetVelocityOfInfinity | returns the speed of propagation at infinite |
| CopyInputData | copies parameters from another EllipticProblem instance |
| IsSymmetricProblem | returns true if the finite element matrix is symmetric |
| IsSymmetricMassMatrix | returns true if the mass matrix is symmetric |
| IsComplexProblem | returns true if the equation needs to be solved with complex numbers |
| ComputeMeshAndFiniteElement | constructs the mesh and finite element classes |
| PerformOtherInitializations | performs other initializations before computing the finite element matrix |
| SetTypeEquation | sets which formulation is used to solve the current equation |
Methods of class VarComputationProblem_Base
The class VarComputationProblem_Base is an abstract class that is used for the assembly of matrices (see details in the description of AssembleMatrix). Below we list the methods of this class, most of them are virtual and are overloaded in the derived classes.
| GetThresholdMatrix | returns the threshold used to drop negligible entries of the matrix |
| SetThresholdMatrix | sets the threshold used to drop negligible entries of the matrix |
| GetNbElt | returns the number of elements |
| GetNbRows | returns the number of rows of the assembled matrix |
| ComputeElementaryMatrix | computes the elementary matrix of a given element |
| GetInternalNodesElement | retrieves degrees of freedom that can be eliminated for a given element |
| GetNewCondensationSolver | constructs a new object handling static condensation |
Methods of class VarComputationProblem (class inherited from VarComputationProblem_Base)
The class VarComputationProblem implements the computation of finite element matrices.
| UseMatrixFreeAlgorithm | returns true if the finite element matrix will not be stored |
| IsSymmetricGlobalMatrix | returns true if the finite element matrix is symmetric |
| GetStorageFiniteElementMatrix | returns the type of storage for the finite element matrix |
| SetStorageFiniteElementMatrix | sets the type of storage for the finite element matrix |
| SetSymmetricElementaryMatrix | sets the symmetry of elementary matrices |
| SetLeafStaticCondensation | informs Montjoie to effectively perform (or not) the static condensation. |
| GetLeafStaticCondensation | returns true if the static condensation has to been effectively performed |
| LightStaticCondensation | returns true if a light static condensation is used |
| GetSymmetrizationUse | returns true if a symmetrization is used |
| SetSymmetrizationUse | enables/disables the use of symmetrization |
| SetHomogeneousDirichlet | enables/disables homogeneous Dirichlet conditions |
| IsHomogeneousDirichlet | returns true if only homogeneous Dirichlet conditions are present |
| SetPrintLevel | sets the verbosity level |
| GetMemorySize | returns the memory used by the object in bytes |
| SetPrintLevel | sets the verbosity level |
| AddMatrixWithBC | adds the finite element matrix (boundary conditions included) |
| AddMatrixFEM | adds the finite element matrices (without boundary conditions) |
| ComputeDiagonalMatrix | computes the diagonal of the finite element matrix |
| IsSymmetricElementaryMatrix | returns true if the elementary matrices are symmetric |
| IsDiagonalElementaryMatrix | returns true if the elementary matrices are diagonal |
| IsSparseElementaryMatrix | returns true if the elementary matrices are sparse |
| GetStaticCondensedRows | fills rows that can be condensed |
| AddElementaryFluxesDG | adds terms due to numerical fluxes (Discontinuous Galerkin formulations) |
| UpdateShiftAdimensionalization | updates the shift used for eigenvalue computations due to adimensionalization |
| UpdateEigenvaluesAdimensionalization | updates the eigenvalues due to adimensionalization |
| FindIntervalDofSignSymmetry | finds rows that are multiplied by -1 to obtain a symmetric matrix |
| ModifySourceSymmetry | modifies the right hand side because of symmetrization |
| GetNewIterativeMatrix | constructs a new iterative matrix (to perform the matrix-vector product with finite element matrix) |
| GetNewLinearSolver | constructs a new linear solver (to solve the finite element matrix) |
| GetNewPreconditioning | constructs a new preconditioning (used to solve the finite element matrix) |
Public attributes of class VarGeometryProblem (class inherited from VarProblem_Base)
| mesh | mesh used for the simulations |
| Glob_PointsQuadrature | quadrature points for all the elements (if stored) |
| write_quadrature_points | if true, quadrature points are written in a file |
| write_quad_points_pml | if true, quadrature points (of PMLs) are written in a file |
| Glob_jacobian | Determinant of jacobian matrices on quadrature points |
| Glob_decomp_jacobian | Decomposition of the determinant of jacobian matrices on a polynomial basis |
| Glob_normale | Outgoing normales on quadrature points of the boundaries of the mesh |
| Glob_dsj | Surface integration elements on quadrature points of the boundaries of the mesh |
| OrthogonalElement | type of orthogonality for each element |
| Glob_DFjm1 | inverse of jacobian matrices (multiplied by the determinant) |
| IsNewFace | true if the face j of element i has not been considered |
Methods of class VarGeometryProblem (class inherited from VarProblem_Base)
| GetReferenceInfinity | returns the reference for the infinity medium |
| GetWaveVector | returns the wave vector |
| SetWaveVector | sets the wave vector |
| GetPolarization | returns the polarization vector |
| GetPolarizationGrad | returns the polarization vector (used for gradient of Dirac) |
| GetPhaseOrigin | returns the origin of the phase (for plane waves) |
| SetPolarization | sets the polarization vector |
| FinalizeComputationVaryingIndices | method called after the computation of physical coefficients |
| AllocateMassMatrices | allocation for arrays storing geometric quantities needed for the computation of the finite element matrix |
| DoNotComputeGrid | the interpolation grid is not computed when calling ComputeMeshAndFiniteElement |
| GetLocalUnknownVector | extracts the local components of u on an element of the mesh |
| AddLocalUnknownVector | adds a local (with only values on degrees of freedom of an element of the mesh) vector to the global vector |
| ModifyLocalComponentVector | intermediary function used by GetLocalUnknownVector |
| ModifyLocalUnknownVector | intermediary function used by AddLocalUnknownVector |
| GetGlobalUnknownVector | modification of local projection on reference element to obtain a global projection (respecting signs and orientations of global dofs) |
| InsidePML | returns true if the i-th element belongs to PMLs |
| GetNbComponentsType | returns the number of components for a given type |
| GetNbComponentsGradType | returns the number of components for the gradient for a given type |
| GetNbComponentsAll | returns the number of components for all the unknowns |
| GetNbComponentsGradientAll | returns the number of components for the gradients of all unknowns |
| GetNbComponentsHessianAll | returns the number of components for the hessians of all unknowns |
| GetMeshNumbering | gives access to the mesh numbering |
| WriteNodalPointsMesh | writes nodal points of the mesh in a file understood by write_index |
| LocalizePointsBoundaryElement | localize points of the boundary on an element |
| UseNumericalIntegration | if true, quadrature points are needed to compute integrals because of varying coefficients |
| FaceHasToBeConsideredForBoundaryIntegral | if true the i-th is involved in a boundary integral of the variational formulation |
| GetWeightedJacobian | returns the weighted jacobian on a given quadrature point |
| GetSurfaceWeightedJacobian | returns the weighted jacobian on a given quadrature point of the surface |
| GetInverseJacobianMatrix | retrieves the inverse of jacobian matrix on a given quadrature point |
| FillQuadratureJacobian | fills jacobian matrices on quadrature points |
| ComputeLocalMassMatrix | computes geometric quantities (jacobians, quadrature points, etc) for a single element |
| ComputeMassMatrix | computes geometric quantities Ji, DFi, normale on quadrature points, etc needed for the computation of the finite element matrix |
| ClearMassMatrix | clears arrays containing geometric quantities Ji, DFi, etc |
| ComputeVariableOrder | computes the order for each element |
| GetPhysicalCoefficientMesh | returns the mesh associated with a given file name |
| GetPhysicalCoefInterp | returns the projector for a given order |
| GetPhysicalCoefInterpSurf | returns the surfacic projector for a given order |
| CheckInputMesh | checks and modifies if necessary the initial mesh |
| GetVaryingIndices | retrieves physical indices that are varying |
| ComputeStoreCoefficientsPML | computes and stores damping coefficient for an element of PMLs |
| PointsQuadInsideND | returns interior quadrature points of element i |
| PointsQuadratureBoundary | returns quadrature points on a boundary of an element |
| PointsDofBoundary | returns dof points on a boundary of an element |
| GetShapeElement | returns the geometric finite element associated with a given element |
| ConstructFiniteElement | constructs finite element classes |
| UpdateInterpolationElement | updates the finite element classes (if orders in the mesh changed) |
| ClearFiniteElement | clears finite element classes |
| SplitMeshForParallelComputation | splits the mesh into several subdomains, and send each subdomain to a different processor, and constructs dof numbering |
| ComputeNumberOfDofs | computes the number of degrees of freedom |
| PutOtherGlobalDofs | computes the number of degrees of freedom in parallel |
| CheckContinuity | checks continuity of basis functions (or continuity of tangential traces for edge elements) |
| PartMeshTransmission | parts the mesh due to transmission conditions |
| TreatTransmission | treats transmission conditions |
| SendTransmissionDofs | sends degrees of freedom of due to transmission conditions (in parallel) |
| DistributeTransmissionDofs | distributes degrees of freedom due to transmission conditions between processors |
| TreatGibc | Treats Gibc (Generalized Impedance Boundary Conditions) |
| InitGibcReferences | initializes references for Gibc conditions |
| ComputeEnHnOnBoundary | computes the trace of electric and magnetic field on the boundary |
The class DistributedProblem
Public attributes of class DistributedProblem
| comm_group_mode | MPI communicator for nodes sharing the computation of the same mode |
Public methods of class DistributedProblem (class inherited from VarGeometryProblem)
| GetNbMainUnknownDof | returns the number of degrees of freedom for the main unknown u |
| GetDofNumberOnElement | returns the number of degrees of freedom for a given element |
| GetScalarDofNumberOnElement | returns the number of degrees of freedom for a given element |
| GetNbGlobalMeshDof | returns the global number of degrees of freedom for a mesh numbering |
| GetNbGlobalDofPML | returns the global number of degrees of freedom associated with PMLs for a mesh numbering |
| GetNbGlobalDof | returns the global number of degrees of freedom for all the problem |
| GetOffsetGlobalUnknownDof | returns the cumulated global number of degrees of freedom for an unknown |
| GetNbGlobalUnknownDof | returns the global number of degrees of freedom for an unknown |
| GetNbGlobalCondensedDof | returns the global number of degrees of freedom for an unknown (after static condensation) |
| GetGlobalDofNumber | returns the global number of a local degree of freedom |
| GetNbPointsQuadratureNeighbor | returns the number of quadrature points on the interfaces between subdomains |
| GetNbSubdomains | returns the number of subdomains in interaction with the current subdomain |
| GetNbProcPerMode | returns the number of processors involved in the computation of a mode |
| GetRankMode | returns the rank of the current processor (between processors solving a mode) |
| GetProcMatchingNeighbor | returns the list of processors that are connected with the current processor |
| GetOriginalMatchingDofNeighbor | returns the list of degrees of freedom matching dofs of another processors |
| GetElementNumberNeighboringFace | returns the global number of the element adjacent to a neighboring face |
| GetOffsetNeighboringFace | returns the index of the first quadrature point on the i-th neighboring face |
| GetProcessorNeighboringFace | returns the rank of the processor adjacent to a neighboring face |
| GetLocalPositionNeighboringFace | returns the local position of the face within the element adjacent to a neighboring face |
| GetRotationNeighboringFace | returns the difference of orientation between the two elements sharing a neighboring face |
| GetOrderEltNeighboringFace | returns the order of the element adjacent to a neighboring face |
| GetTypeEltNeighboringFace | returns the hybrid type of the element adjacent to a neighboring face |
| GetNodleNeighboringFace | returns the dof numbers of the element adjacent to a neighboring face |
| GetNodlePmlNeighboringFace | returns the dof numbers (between PML dofs) of the element adjacent to a neighboring face |
| GetRefDomainNeighboringFace | returns the reference of the element adjacent to a neighboring face |
| GetSizeOffsetDofV | returns the length of the array storing offset for vectorial dofs |
| GetOffsetDofV | returns the offset for vectorial dofs for a given element |
| SetOffsetDofV | sets the offset for vectorial dofs for a given element |
| GetNbOverlappedDof | returns the number of overlapped dofs (belonging to another processor) |
| GetOverlappedDofNumber | returns the number of a given overlapped dof (belonging to another processor) |
| GetOverlappedProcNumber | returns the processor that owns a given overlapped dof |
| AllocateDistributedVector | constructs a new distributed vector with data of a sequential vector |
| NullifyDistributedVector | nullifies data contained in a distributed vector and delets the pointer |
| SetEpartSplitting | sets manually how the mesh is split into subdomains (for parallel computation) |
| SaveEpartSplitting | saves the array epart, that stores the processor number for each element |
| GetMemoryUsed | retrieves the memory used by the different variables |
| DisplayMemoryUsed | displays the memory used by the different variables |
| FindElementsInsidePML | marks elements inside PMLs |
| GetNodleElement | returns the numbers of the degrees of freedom of a given element |
| AddDomains | assembles a vector (values associated with dofs shared by several processors are summed) |
| ReduceDistributedVector | reduces a vector (reduction operation is performed on shared dofs) |
| AssembleDirichlet | assembles a vector only for Dirichlet dofs |
| ReduceDirichlet | reduces a vector for Dirichlet dofs |
| ConstructDirichletComm | updates arrays for Dirichlet dofs (for AssembleDirichlet/ReduceDirichlet) |
| ExchangeDomains | values associated with dofs shared by several processors are exchanged |
| ExchangeRelaxDomains | values associated with dofs shared by several processors are exchanged (with relaxation) |
| ExchangeQuadRelaxDomains | values associated with quadrature points shared by several processors are exchanged (with relaxation) |
| ExchangeUfaceDomains | exchanges values of the solution on quadrature points of neighboring faces |
| GetUfaceDomains | completes transfer of values of the solution on quadrature points of neighboring faces |
| SplitSubdomains | splits the mesh into several subdomains, and send each subdomain to a different processor |
| ReduceDistributedVectorFace | reduces a vector (reduction operation is performed on shared faces) |
| ComputeLocalProlongation | compute the local prolongation operator |
| GetNewEllipticProblem | constructs an object of the leaf class EllipticProblem |
| CopyFiniteElement | copies the finite elements stored in another class |
| ComputeEnHnNodal | computes E x n and H x n on nodal points |
Public methods of class VarProblem (class inherited from VarComputationProblem, DistributedProblem and VarFiniteElement)
The class VarProblem is a base class for solving time-harmonic (or steady) problems. It is mainly containing the methods specific to finite elements. In older versions of Montjoie, this class was depending on the type of finite element. Now, this class only depends on the dimension. It is an abstract class, the leaf class EllipticProblem should be instantiated. Below, we list the methods specific to this class.
| ComputeDofCoordinates | computes the coordinates of degrees of freedom |
| ComputeReferenceGradientElement | computes the gradient (on the reference element) from components on degrees of freedom |
| GetMassMatrixType | returns the nature of the mass matrix (sparse, diagonal, block-diagonal, etc) |
| GetElementaryMatrixType | returns 0 if the elemenary matrix is dense, 1 if it is sparse |
| ComputeEnHnQuadrature | computes E x n and H x n on quadrature points |
| GetPrintLevel | returns the verbosity level |
Public methods of class VarHarmonic (class inherited from VarProblem, VarBoundaryCondition, VarOutputProblem and VarSourceProblem)
The class VarHarmonic is the base class for time-harmonic problems (or steady problems). The leaf class will be an instance of EllipticProblem. The class VarHarmonic is a template class that depends on the type of equation. In practice, the class VarHarmonic is split into two classes : the class VarHarmonic_Base (templated with the dimension and real/complex numbers) and the class VarHarmonic (templated with the type of equation). The aim of this decomposition, is to avoid a large number of instantiations (with most of methods contained in VarHarmonic_Base).
| Restart | restarts a computation with the same object |
| ConstructAll | constructs all what is needed for the computation of finite element matrices |
| RunAll | runs a complete simulation (from reading the input file until writing the results in output files) |
| GetInverseSquareRootMassMatrix | computes the inverse of the square root of mass matrix (if diagonal) |
| GetMassMatrix | computes the mass matrix (if diagonal) |
| SetComputationFarPoints | sets the points outside the computational domain |
| GetNewTransparentSolver | constructs a new solver (for handling transparent condition) |
| GetNewEigenSolver | constructs a new eigenvalue solver (for the computation of eigenvalues and eigenvectors) |
| GetNewPolynomialEigenSolver | constructs a new eigenvalue solver in the case of polynomial eigenproblem |
| GetGenericImpedanceFunction | returns the object implementing impedance boundary condition |
| GetAbsorbingImpedanceFunction | returns the object implementing absorbing boundary condition |
Public attributes of class VarHarmonic
| fct_impedance_absorbing | object implementing absorbing boundary condition (impedance coefficient) |
| fct_impedance_generic | object implementing impedance boundary condition |
| fct_impedance_high_conduc | object implementing high-order conductivity condition |
| output_rcs_param | object handling computation of Radar Cross Sections (RCS) |
| var_transmission | object handling impedance transmission conditions |
| var_gibc | object handling generalized impedance boundary conditions |
Axisymmetric computations
The class VarAxisymProblem is the base class for axisymmetric problems. It contains methods specific to the treatment of the axisymmetric case. For time-harmonic solution, the solution is expanded in Fourier modes :
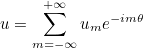
Each mode um can be solved independently. The class EllipticProblem will inherit the methods of the class VarAxisymProblem for equations used to solve axisymmetric problems (e.g. HelmholtzEquationAxi, HarmonicMaxwellEquation_HcurlAxi).
Public methods of class VarAxisymProblem
| GetFourierMode | returns e-im θ (or cos(m θ) for real numbers) |
| IsVertexOnAxis | returns true is the vertex i is located on the axis of revolution |
| IsElementNearAxis | returns true is the element i has a vertex on the axis of revolution |
| NumberOfModesToBeComputed | returns true is the number of Fourier modes has to be computed |
| GetModeThreshold | returns the threshold used to drop Fourier modes |
| GetBessel_Value | returns the value of Bessel function Jn for a quadrature point |
| CheckSectionMeshAxi | checks if the mesh is valid for an axisymmetric configuration |
| ComputeDofOnAxe | computes degrees of freedom located on the axis of revoluation |
| Get_KwavePerp_Kz_Phase | Computes k⟂, kz for a given wave vector |
| ComputeListMode | Computes the number of modes to obtain an accurate solution (for RCS) |
| ComputeNbModes_Generic | Computes the number of modes to obtain an accurate solution for a given plane wave |
| InitBesselArray | Precomputes Bessel functions for all plane waves (for RCS) |
| InitRcs | Initalizes the computation of Radar Cross Sections (RCS) |
| GetNbRightHandSide | returns the number of right hand sides required for the given RCS) |
Matrix-vector product with finite element matrix
The finite element matrix is represented by the class FemMatrixFreeClass. This class may store the matrix or not, depending on the finite element, the order of approximation, and the solved equation. The method MltVector is overloaded for this class.
// The definition of the problem is constructed via EllipticProblem class
EllipticProblem<TypeEquation> var;
var.InitIndices(100);
var.SetTypeEquation("HELMHOLTZ");
ReadInputFile(input_file, var);
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations();
var.ComputeMassMatrix();
var.ComputeQuasiPeriodicPhase();
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Complex_wp> nat_mat;
Matrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// By default, alpha = beta = gamma = 1
// but you can change them
Complex_wp alpha = 2.0, beta = 0.5, gamma = 0.25;
nat_mat.SetCoefMass(alpha);
nat_mat.SetCoefDamping(beta);
nat_mat.SetCoefStiffness(gamma);
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Real_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// then you can compute the matrix-vector product
Vector<Complex_wp> x(Ah->GetM()), y(Ah->GetM()); x.FillRand();
Ah->MltVector(x, y);
delete Ah;
The function MltAddFree is overloaded in the leaf classes (depending on the equation).
Public attributes of FemMatrixFreeClass
| mat_boundary* | additional sparse matrix coming from boundary conditions or other models |
| mat_iterative* | main sparse matrix if the finite element is stored |
| matCSR_boundary* | mat_boundary in CSR (Compressed Sparse Row) format |
| matCSR_iterative* | mat_iterative in CSR (Compressed Sparse Row) format |
| var | problem associated with the finite element matrix |
Methods of FemMatrixFreeClass (inherited from VirtualMatrix)
| constructor of FemMatrixFreeClass | |
| SetCoefficientDirichlet | changes coefficient on diagonal entry for Dirichlet dofs |
| SetCoefficientMatrix | changes mass, stifness and damping coefficients |
| GetCoefMass | returns the coefficient associated with the mass matrix |
| IsSymmetric | returns true if the current matrix is symmetric |
| FormulationDG | returns the type of discontinuous Galerkin formulation |
| SetCondensedSolver | sets the condensed solver used to compute the condensed matrix |
| DirichletDofIgnored | returns true if Dirichlet dofs will be ignored in the matrix vector product |
| IgnoreDirichletDof | informs that Dirichlet dofs should be ignored |
| SetScaling | sets scalings to be used for the rows and columns of the matrix |
| SucceedInAffectingPointer | returns true if the method succeeded in addressing the pointer to the current matrix |
| InitSymmetricMatrix | initializes the matrix as a symmetric matrix |
| InitUnsymmetricMatrix | initializes the matrix as a non-symmetric matrix |
| ApplyLeftScaling | applies row scaling on a vector |
| ApplyRightScaling | applies column scaling on a vector |
| CompressMatrix | converts sparse matrices to CSR matrices to reduce memory usage |
| AddExtraBoundaryTerms | adds terms due to boundary conditions |
| SetNbDirichletCondition | sets the number of right hand sides (for Dirichlet conditions) |
| ApplyDirichletCondition | modifies the right hand side such that it vanishes for Dirichlet dofs |
| MltAddHetereogeneousDirichlet | multiplies the matrix with only columns associated with Dirichlet dofs |
| SetDirichletCondition | modifies the matrix due to Dirichlet condition |
| InitDirichletCondition | initializes Dirichlet condition |
| ImposeDirichletCondition | imposes a null Dirichlet condition to the vector given on input |
| MltAddFree | performs the matrix-vector product (matrix-free implementation) |
| GetExtrapolVariables | returns the intermediary object used to perform the matrix vector product |
Methods of MatrixVectorProductLevel
| SetLevel | specifies which elements are to be considered for the matrix-vector product |
| GetLevelArray | returns the element numbers for each level |
| SetLevelArray | sets the element numbers for each level |
| GetNbElt | returns the number of elements for a given level |
| GetElementNumber | returns the element number of the selected level |
| GetLocalElementNumber | returns the local element number of the selected level |
| TreatElement | returns true if the element i should be considered in the matrix-vector product |
| SetNbElt | sets the number of elements in the mesh |
| GetMemorySize | returns the memory used by the object in bytes |
Methods of CondensationBlockSolver_Base
| ModifyElementaryMatrix | applies the static condensation to an elementary matrix |
| SetElementNumber | sets the element number (global and condensed) |
| GetCondensedElementNumber | returns the condensed number of the selected element |
| GetGlobalElementNumber | returns the global number of the selected element |
| SetNbCondensedElt | sets the number of condensed elements |
| GetNbCondensedElt | returns the number of condensed elements |
| GetMemorySize | returns the memory used to store the object (in bytes) |
Methods of GlobalGenericMatrix
| GetCoefMass | returns the mass coefficient |
| GetCoefStiffness | returns the stiffness coefficient |
| GetCoefDamping | returns the damping coefficient |
| SetCoefMass | sets the mass coefficient |
| SetCoefStiffness | sets the stiffness coefficient |
| SetCoefDamping | sets the damping coefficient |
AssembleMatrix
Syntax
| void AssembleMatrix( | Matrix& A, Matrix& mat_elem, GlobalGenericMatrix nat_mat |
| VarComputationProblem_Base& var, CondensationBlockSolver_Base& solver, int offset_row, int offset_col) |
Parameters
- A (inout)
- matrix to modify
- mat_elem(inout)
- elementary matrix
- nat_mat (in)
- coefficients
- var (inout)
- class defining the computation of elementary matrices
- solver (inout)
- solver (for static condensation)
- offset_row (in)
- offset for row numbers
- offset_col (in)
- offset for column numbers
This function adds elementary matrices to the global matrix A. The elementary matrices are computed by AssembleMatrix by calling the method ComputeElementaryMatrix of the object var given as a parameter. Below we reproduce an example located in the file src/Program/Unit/Computation/assemble_matrix.cc. If the global matrix A is not allocated, the function will allocate it and fill it.
Example :
// class overloading VarComputationProblem_Base to define elementary matrices
class MyExample : public VarComputationProblem_Base
{
int Nx, Ny; Real_wp dx, dy;
public :
MyExample(double Lx, double Ly, int Nx_, int Ny_)
{
Nx = Nx_; Ny = Ny_;
dx = Lx / Nx; dy = Ly / Ny;
}
// number of elementary matrices to compute
int GetNbElt() const { return Nx*Ny; }
// number of rows of the global matrix
int GetNbRows() const { return (Nx+1)*(Ny+1); }
// verbosity level
int GetPrintLevel() const { return 0; }
// elementary matrix for real coefficients
// i : element number, num_row : row numbers of the element i
// mat_elem : elementary matrix, solver : static condensation solver, coef : coefficients
void ComputeElementaryMatrix(int i, IVect& num_row,
VirtualMatrix<Real_wp>& mat_elem,
CondensationBlockSolver_Base<Real_wp>& solver,
const GlobalGenericMatrix<Real_wp>& coef)
{
// basic exemple alpha M + beta K
// where M is a mass matrix and K stiffness matrix
mat_elem.Reallocate(4, 4);
mat_elem.Zero();
int ie = i %Nx, je = i / Nx;
// row numbers of the considered element
num_row.Reallocate(4);
num_row(0) = je*(Nx+1) + ie;
num_row(1) = num_row(0) + 1;
num_row(2) = num_row(1) + Nx;
num_row(3) = num_row(2) + 1;
Real_wp K00 = 0.5*dy/dx + 0.5*dx/dy;
Real_wp K01 = -0.5*dy/dx, K10 = -0.5*dx/dy;
Real_wp M00 = 0.25*dx*dy;
Real_wp alpha = coef.GetCoefMass();
Real_wp beta = coef.GetCoefStiffness();
mat_elem.SetEntry(0, 0, beta*K00 + alpha*M00);
mat_elem.SetEntry(0, 1, beta*K01);
mat_elem.SetEntry(0, 2, beta*K10);
mat_elem.SetEntry(1, 1, beta*K00 + alpha*M00);
mat_elem.SetEntry(1, 0, beta*K01);
mat_elem.SetEntry(1, 3, beta*K10);
mat_elem.SetEntry(2, 2, beta*K00 + alpha*M00);
mat_elem.SetEntry(2, 3, beta*K01);
mat_elem.SetEntry(2, 0, beta*K10);
mat_elem.SetEntry(3, 3, beta*K00 + alpha*M00);
mat_elem.SetEntry(3, 2, beta*K01);
mat_elem.SetEntry(3, 1, beta*K10);
}
// elementary matrix for complex matrices
void ComputeElementaryMatrix(int i, IVect& num_row,
VirtualMatrix<Complex_wp>& mat_elem,
CondensationBlockSolver_Base<Complex_wp>& solver,
const GlobalGenericMatrix<Complex_wp>& coef)
{
cout << "Not implemented" << endl;
abort();
}
};
int main(int argc, char** argv)
{
InitMontjoie(argc, argv);
MyExample var(2.0, 2.0, 5, 5);
// global matrix
Matrix<Real_wp, Symmetric, ArrayRowSymSparse> Aref;
Matrix<Real_wp, Symmetric, RowSymPacked> mat_elem; // elementary matrix
CondensationBlockSolver_Base<Real_wp> cond_solver; // object to handle static condensation
GlobalGenericMatrix<Real_wp> nat_mat; // coefficients
// setting coefficients (if needed)
nat_mat.SetCoefMass(0.4); nat_mat.SetCoefStiffness(1.3);
// we assemble the matrix A
AssembleMatrix(A, mat_elem, nat_mat, var, cond_solver, 0, 0);
}
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
ModifyElementaryMatrix
Syntax
| void ModifyElementaryMatrix( | int i, IVect& num_dof, Matrix& mat_elem, GlobalGenericMatrix nat_mat) |
Parameters
- i (in)
- element number
- num_dof (inout)
- row numbers that are kept
- mat_elem (inout)
- elementary matrix that can be modified due to static condensation
- nat_mat (in)
- coefficients
This methods modifies the elementary matrix previously computed by the method ComputeElementaryMatrix. If static condensation is applied, it should produce a smaller matrix with only rows that cannot be eliminated. The parameter num_dof contains the rows that are kept.
Example :
// class overloading CondensationBlockSolver_Base
class MySolver<Real_wp> : public CondensationBlockSolver_Base<Real_wp>
{
VectReal_wp schur_coef;
public :
void ModifyElementaryMatrix(int i, IVect& num_ddl, VirtualMatrix<Real_wp> mat_elem, const GlobalGenericMatrix<Real_wp>& nat_mat)
{
int j = mat_elem.GetM()-1;
// for instance the last dof is eliminated
VectReal_wp last_row, last_col
mat_elem.GetDenseRow(j, last_row);
mat_elem.GetDenseCol(j, last_col);
Real_wp invA22 = Real_wp(1) / last_row(j);
// updating Schur complement
mat_elem.Resize(j, j);
for (int i = 0; i < j; i++)
if (last_row(i) != Real_wp(0))
for (int k = 0; k < j; k++)
if (last_col(k) != Real_wp(0))
mat_elem.AddInteraction(k, i, -invA22*last_row(i)*last_col(k));
// last dof is removed
num_ddl.Resize(j);
// we can store invA22
schur_coef(i) = invA22;
}
};
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetTreatmentStiffnessInside
Syntax
| void SetTreatmentStiffnessInside( | bool t) |
This method informs if there are stiffness terms to handle for the static condensation. It is used by local implicit schemes.
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetElementNumber
Syntax
| void SetElementNumber(int local_num , int global_num ) |
This method sets the local element number (among condensed elements) and the global element number. Usually these two numbers are equal (if all the elements contribute to the condensed matrix).
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetCondensedElementNumber
Syntax
| int GetCondensedElementNumber() const |
This method returns the current condensed element number.
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetGlobalElementNumber
Syntax
| int GetGlobalElementNumber() const |
This method returns the current global element number.
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetNbCondensedElt
Syntax
| int GetNbCondensedElt() const |
This method returns the number of condensed elements (elements that contribute to the condensed matrix).
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetNbCondensedElt
Syntax
| void SetNbCondensedElt(int n ) |
This method sets the number of condensed elements (elements that contribute to the condensed matrix).
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetMemorySize
Syntax
| size_t GetMemorySize() const |
This method returns the memory used to store the object (in bytes).
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetCoefMass
Syntax
| T GetCoefMass() const |
This method returns the coefficient associated with the mass matrix. If the equation is used in time-domain, it corresponds to the coefficient for the second derivatives in time. If the equation only involves first derivatives in time, the coefficient applies to first derivatives. This coefficient is the coefficient α detailed in the equation below.

Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetCoefDamping
Syntax
| T GetCoefDamping() const |
This method returns the coefficient associated with the damped matrix. If the equation is used in time-domain, it corresponds to the coefficient for the first derivatives in time if the equation is a second-order formulation in time. If the equation is a first-order formulation, it corresponds to coefficients associated with damping terms. It correspdonds to the coefficient β in the equations below.
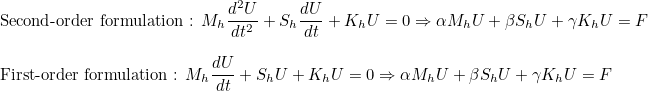
Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetCoefStiffness
Syntax
| T GetCoefStiffness() const |
This method returns the coefficient associated with the stiffness matrix. If the equation is used in time-domain, it corresponds to the coefficient for terms without time-derivatives. It correspdonds to the coefficient γ in the equations below.
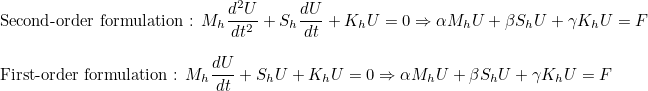
Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetCoefMass
Syntax
| void SetCoefMass(T coef) const |
This method sets the coefficient associated with the mass matrix. This coefficient is the coefficient α detailed in the description of GetCoefMass.
Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetCoefDamping
Syntax
| void SetCoefDamping(T coef) const |
This method sets the coefficient associated with the damped matrix. This coefficient is the coefficient β detailed in the description of GetCoefDamping.
Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetCoefStiffness
Syntax
| void SetCoefStiffness(T coef) const |
This method sets the coefficient associated with the stiffness matrix. This coefficient is the coefficient γ detailed in the description of GetCoefStiffness.
Example :
GlobalGenericMatrix<Real_wp> nat_mat; // you can set coefficients nat_mat.SetCoefMass(Real_wp(0.4)); nat_mat.SetCoefDamping(Real_wp(0.8)); nat_mat.SetCoefStiffness(Real_wp(1.5)); // and retrieve them Real_wp m = nat_mat.GetCoefMass(); Real_wp sig = nat_mat.GetCoefDamping(); Real_wp s = nat_mat.GetCoefStiffness();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetLevel
Syntax
| void SetLevel(int lvl) |
This method sets the level, such that the matrix-vector product will be performed only for elements of the selected level. There are predefined levels (which correspond to negative numbers):
- ALL_LEVELS : all the elements of the mesh are considered
- LVL_PML : all the elements in PMLs are considered
- LVL_NOPML : all the elements outside PMLs are considered
Example :
// class for solving acoustic equation
HyperbolicProblem<AcousticEquation<Dimension2> > var;
// assuming that var is correctly constructed
// you can retrieve the different levels
// each level is usually associated with an area with a given time step
MatrixVectorProductLevel& list_level = var.GetTimeLevelDistribution();
// you can select a level with SetLevel
list_level.SetLevel(1);
// and loop over selected elements
for (int i0 = 0; i0 < list_level.GetNbElt(); i0++)
{
int i = list_level.GetElementNumber(i0);
// and perform the computation for the element i
}
// to select a predefined level
list_level.SetLevel(MatrixVectorProductLevel::ALL_LEVELS);
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetLevelArray
Syntax
| Vector<IVect> GetLevelArray() |
This method returns the list of elements for each level.
Example :
// class for solving acoustic equation
HyperbolicProblem<AcousticEquation<Dimension2> > var;
// assuming that var is correctly constructed
// you can retrieve the different levels
// each level is usually associated with an area with a given time step
MatrixVectorProductLevel& list_level = var.GetTimeLevelDistribution();
// you can select a level with SetLevel
list_level.SetLevel(1);
// you can display the elements of each level
Vector<IVect>& lvl_array = list_level.GetLevelArray();
cout << "Elements for level 0 = " << lvl_array(0) << endl;
cout << "Elements for level 1 = " << lvl_array(1) << endl;
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetLevelArray
Syntax
| void SetLevelArray(Vector<IVect>& liste ) |
This method sets the list of elements for each level.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetNbElt
Syntax
| int GetNbElt() |
| int GetNbElt(int level ) |
This method returns the number of elements of a given level. If no argument is given, it returns the number of elements of the selected level (with method SetLevel).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
// number of elements for level 1 ?
int n1 = prod_level.GetNbElt(1);
// setting a level
prod_level.SetLevel(2);
// and number of elements on the selected level (2 here)
int n2 = prod_level.GetNbElt();
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
SetNbElt
Syntax
| void SetNbElt(int num_elt , int lnum_elt_pml ) |
This method sets the number of elements (in total) and the number of elements inside PML.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
// you can select all elements inside the PML
prod_level.SetLevel(MatrixVectorProductLevel::LVL_PML);
// and loop over them
int n0 = prod_level.GetNbElt()
for (int i0 = 0; i0 < n0; i0++)
{
int i = prod_level.GetElementNumber(i0);
}
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetElementNumber
Syntax
| int GetElementNumber(int i ) |
This method returns the global element number of the i-th element of the selected level.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
// you can select all elements inside the PML
prod_level.SetLevel(MatrixVectorProductLevel::LVL_PML);
// and loop over them
int n0 = prod_level.GetNbElt()
for (int i0 = 0; i0 < n0; i0++)
{
int i = prod_level.GetElementNumber(i0); // global element number
}
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
GetLocalElementNumber
Syntax
| int GetLocalElementNumber() |
This method returns the local element number. This method is used in an alternative way to browse the elements of a given level, as detailed in the example below.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
// you can select all elements inside the PML
prod_level.SetLevel(MatrixVectorProductLevel::LVL_PML);
// and loop over them
int n0 = prod_level.GetNbElt()
// first method : loop over local numbers
for (int i0 = 0; i0 < n0; i0++)
{
int i = prod_level.GetElementNumber(i0); // global element number (in the mesh)
}
// second method : loop over global numbers
// in that case, you need to browse these elements in ascending order
prod_level.SetLevel(0);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
if (var.TreatElement(i))
{
// you can retrieve the local number i0
int i0 = prod_level.GetLocalElementNumber();
}
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
TreatElement
Syntax
| bool TreatElement(int i ) |
This method returns true is the element i belongs to the selected level. This method is used in an alternative way to browse the elements of a given level, as detailed in the example below.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
MatrixVectorProductLevel prod_level;
// setting the number of elements (total number and number in PMLs)
prod_level.SetNbElt(var.mesh.GetNbElt(), var.GetNbEltPML());
// setting the element numbers for differents levels
Vector<IVect> list_level(3);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
list_level(i%3).PushBack(i)
prod_level.SetLevelArray(list_level);
// you can select all elements inside the PML
prod_level.SetLevel(MatrixVectorProductLevel::LVL_PML);
// and loop over them
int n0 = prod_level.GetNbElt()
// first method : loop over local numbers
for (int i0 = 0; i0 < n0; i0++)
{
int i = prod_level.GetElementNumber(i0); // global element number (in the mesh)
}
// second method : loop over global numbers
// in that case, you need to browse these elements in ascending order
prod_level.SetLevel(0);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
if (var.TreatElement(i))
{
// you can retrieve the local number i0
int i0 = prod_level.GetLocalElementNumber();
}
// TreatElement can only be used in a loop over all the elements (in ascending order)
// it cannot be used solely to know if a single elements belongs to the selected level
Location :
Computation/AssembleMatrix.hxx
Computation/AssembleMatrix.cxx
print_level
This attribute is the verbosity level. It is usually modified through data file (by inserting a line PrintLevel = lvl).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
// you can modify the attribute manually
var.print_level = 2;
Location :
nb_unknowns
This attribute is the number of unknowns of the solved equation. It cannot be modified, this attribute is actually set in the class defining the equation. It is equal to
- The number of continuous unknowns (that need to be numbered) for a continuous formulation. For instance, for the Helmholtz equation, the number of unknowns is equal to 1 (even though a mixed formulation is used with a discontinuous unknown v).
- The number of discontinuous unknowns for a discontinuous Galerkin formulation. For instance, for the Helmholtz equation (solved with LDG method), the number of unknowns is equal to d+1 (where d is the dimension).
- The number of volume unknowns for HDG. For instance for the Helmholtz equation (solved with HDG method), the number of unknowns is equal to d+1, the surface unknown λ is not counted.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
// you can access to the number of unknowns
int n = var.nb_unknowns;
Location :
nb_unknowns_scal
This attribute is the number of scalar unknowns of the solved equation. It cannot be modified, this attribute is actually set in the class defining the equation. It is equal to
- The number of continuous unknowns (that need to be numbered) for a continuous formulation. For a continuous formulation, nb_unknowns and nb_unknowns_scal are equal. For instance, for the Helmholtz equation, the number of scalar unknowns is equal to 1.
- The number of scalar discontinuous unknowns for a discontinuous Galerkin formulation. For instance, for the Helmholtz equation (solved with LDG method), the number of scalar unknowns is equal to 1 (only unknown u is assumed to be scalar).
- The number of scalar volume unknowns for HDG. For instance for the Helmholtz equation (solved with HDG method), the number of scalar unknowns is equal to 1.
For discontinuous Galerkin formulation, this number is used in order to use staggered time-schemes (with a scalar unknown u and a vectorial unknown v).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the number of "scalar" unknowns
int n = var.nb_unknowns_scal;
Location :
nb_unknowns_vec
This attribute is the number of vectorial unknowns of the solved equation. It cannot be modified, this attribute is actually set in the class defining the equation. It is equal to
- The number of discontinuous unknowns (for a mixed formulation) for a continuous formulation. For instance, for the Helmholtz equation, the number of vectorial unknowns is equal to d where d is the dimension.
- The number of vectorial discontinuous unknowns for a discontinuous Galerkin formulation. For instance, for the Helmholtz equation (solved with LDG method), the number of vectorial unknowns is equal to d (only unknown v is assumed to be vectorial).
- The number of vectorial volume unknowns for HDG. For instance for the Helmholtz equation (solved with HDG method), the number of vectorial unknowns is equal to d.
For discontinuous Galerkin formulation, this number is used in order to use staggered time-schemes (with a scalar unknown u and a vectorial unknown v).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the number of "vectorial" unknowns
int n = var.nb_unknowns_vec;
Location :
nb_unknowns_hdg
This attribute is the number of surface unknowns of the solved equation. It cannot be modified, this attribute is actually set in the class defining the equation. It is significant only for HDG formulation. If an equation is not solved with HDG, it is usually set to 0.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the number of surface unknowns
int n = var.nb_unknowns_hdg;
Location :
nb_components_en
This attribute is the number of components of the trace of the solution. It cannot be modified, this attribute is actually set in the class defining the equation. It is mainly used for the transparent condition, wich needs to compute the solution on a closed surface : the trace of the solution and derivatives. For instance, for Helmholtz equation, it will need to compute u and
 on the surface. For Helmholtz equation, it will be equal to 1, whereas for Maxwell's equations, it is equal to three (in 3-D) because the electric field has three components.
on the surface. For Helmholtz equation, it will be equal to 1, whereas for Maxwell's equations, it is equal to three (in 3-D) because the electric field has three components.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the number of components to store E \times n
int n = var.nb_components_en;
Location :
nb_components_hn
This attribute is the number of components of the trace of the derivative of the solution. It cannot be modified, this attribute is actually set in the class defining the equation. It is mainly used for the transparent condition, wich needs to compute the solution on a closed surface : the trace of the solution and derivatives. For instance, for Helmholtz equation, it will need to compute u and
 on the surface. For Helmholtz equation, it will be equal to 1 (du/dn is scalar), whereas for Maxwell's equations, it is equal to three (in 3-D) because the magnetic field has three components.
on the surface. For Helmholtz equation, it will be equal to 1 (du/dn is scalar), whereas for Maxwell's equations, it is equal to three (in 3-D) because the magnetic field has three components.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the number of components to store H \times n
int n = var.nb_components_hn;
Location :
type_element
This attribute is the type of the finite element to use for the main unknown. This type is an integer that can be equal to 1, 2 or 3 :
- 1 : use of scalar finite element for the main unknown (discretization of H1 or L2 space)
- 2 : use of edge element (discretization of H(curl) space)
- 3 : use of facet element (discretization of H(div) space)
The finite elements classes are described in the section devoted to finite elements. They depend on a template parameter which corresponds to the type of the finite element. The attribute type_element cannot be modified and is defined in the class defining the equation. The main unknown is the unknown associated with the first mesh numbering. Most of solved equations rely on a single mesh numbering.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// you can access to the type of finite element used to solve the equation
int type_elt = var.type_element;
Location :
other_type_element
This attribute is the type of the finite element to use for other unknowns. This type is an integer that can be equal to 1, 2 or 3 :
- 1 : use of scalar finite element for another unknown (discretization of H1 or L2 space)
- 2 : use of edge element (discretization of H(curl) space)
- 3 : use of facet element (discretization of H(div) space)
The finite elements classes are described in the section devoted to finite elements. They depend on a template parameter which corresponds to the type of the finite element. The attribute other_type_element cannot be modified and is defined in the class defining the equation. The main unknown is the unknown associated with the first mesh numbering, while other unknowns are associated with the next mesh numberings. Most of solved equations rely on a single mesh numbering. In that case, the array other_type_element is void. If there are at least two mesh numberings, other_type_element(i) will be the type of the finite element for the i+1-th mesh numbering.
Example :
EllipticProblem<HarmonicMaxwellEquation_HcurlAxi> var;
// you can access to the type of finite element used for the main unknown
int type_elt = var.type_element;
// and additional unknown
int type_elt2 = var.other_type_element(0);
Location :
finite_element_name
This attribute stores the finite element name (used for the main unknown). It corresponds to the parameter given when filling TypeElement in the data file.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;
// after constructing the mesh
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// you can access to the name of finite element
string name_elt = var.finite_element_name ; // should be QUADRANGLE_LOBATTO
Location :
name_other_elements
This attribute stores the finite element name used for other unknowns. It corresponds to the parameter given when filling TypeElement in the data file.
Example :
EllipticProblem<HarmonicMaxwellEquation_HcurlAxi> var;;
// after setting finite element
var.SetTypeElement("QUADRANGLE_HCURL_AXI");
// you can access to the name of finite element
string name_elt = var.finite_element_name ; // for the main unknown
string name_elt2 = var.name_other_elements(0); // and second unknown
Location :
mesh_num_unknown
This attribute stores the mesh numberings to use for each unknown. For most equations with only one mesh numbering, this array is filled with zeros.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
var.InitIndices(20);
var.SetTypeEquation("LAPLACE");
ReadInputFile(name_file, var);
// mesh numbering to use for the unknown 1 ?
int n = var.mesh_num_unknown(1);
Location :
offset_dof_unknown
This attribute stores the cumulated number of degrees of freedom for each unknown. For instance, let us consider three unknowns and N1, N2, N3 degrees of freedom for each of them. offset_dof_unknown will be equal to (0, N1, N1+N2, N1+N2+N3).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// starting row for the first unknown
int n0 = var.offset_dof_unknown(0); // should be 0
// starting row for the second unknown
int n1 = var.offset_dof_unknown(1); // should be equal to N1
// starting row for the third unknown
int off2 = var.offset_dof_unknown(2); // should be equal to N1+N2
Location :
offset_dof_condensed
This attribute stores the cumulated number of degrees of freedom for each unknown (with static condensation). For instance, let us consider three unknowns and N1, N2, N3 condensed degrees of freedom for each of them. offset_dof_condensed will be equal to (0, N1, N1+N2, N1+N2+N3). The condensed number of degrees of freedom is the number of degrees of freedom after static condensation (internal dofs of elements are removed).
Example :
EllipticProblem<ElasticEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "ELASTIC", solver);
// starting row for the first unknown
int n0 = var.offset_dof_condensed(0); // should be 0
// starting row for the second unknown (condensed system)
int n1 = var.offset_dof_condensed(1); // should be equal to N1
// starting row for the third unknown (condensed system)
int off2 = var.offset_dof_condensed(2); // should be equal to N1+N2
Location :
dg_formulation
This attribute stores the type of the formulation used to solve the equation. It can be equal to
- ElementReference_Base::CONTINUOUS :the equation is solved with continuous finite elements.
- ElementReference_Base::DISCONTINUOUS :the equation is solved with discontinuous Galerkin formulation.
- ElementReference_Base::HDG :the equation is solved with Hybridizable Discontinuous Galerkin formulation.
The formulation is specified in the definition of the equation.
Example :
EllipticProblem<ElasticEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "ELASTIC", solver);
// which formulation is used ?
int dg_form = var.dg_formulation;
Location :
sipg_formulation
This attribute is equal to true if Interior Penalty Discontinuous Galerkin is used. If it is false, Local Discontinuous Galerkin is used
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIGP", solver);
// dg_form should be equal to ElementReference_Base::DISCONTINUOUS
int dg_form = var.dg_formulation;
// sipg should be true (LAPLACE_SIPG given in ConstructAll)
bool sipg = var.sipg_formulation;
Location :
compute_dfjm1
This attribute is equal to true if the jacobian matrices will be computed (and stored). For most of equations, they are computed.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// if you want to force that jacobian matrices are stored
var.compute_dfjm1 = true;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIGP", solver);
Location :
alpha_penalization
This attribute is a penalty parameter used in discontinuous Galerkin formulations. It can be modified through PenalizationDG in the data file.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// to know parameter alpha for penalization
Real_wp alpha = var.alpha_penalization;
Location :
delta_penalization
This attribute is a penalty parameter used in discontinuous Galerkin formulations. It can be modified through PenalizationDG in the data file.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// to know parameter alpha for penalization
Real_wp alpha = var.alpha_penalization;
// to know parameter delta for penalization
Real_wp delta = var.delta_penalization;
Location :
upwind_fluxes
If true, upwind fluxes are used in the discontinuous Galerkin formulation. It can be specified through PenalizationDG in the data file. If false, centered fluxes are used with penalty terms. Depending on the penalty coefficients (alpha_penalization, delta_penalization) and the considered equation, it can coincide with upwind fluxes. It is the case for Helmholtz equation, if alpha and delta are set to -1. If alpha and delta are set to zero, and upwind_fluxes is false, it correspond to pure centered fluxes (without penalty terms).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// to know if upwind fluxes are used
Real_wp upwind = var.upwind_fluxes;
Location :
automatic_choice_penalization
If this attribute is true, the penalty coefficient is automatically chosen (depending on the order of approximation and the mesh size). It is usually set through CoefficientPenalization in the data file. It is significant only for Interior Penalty Discontinuous formulation.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// to know if the penalty coefficients are automatically chosen
bool auto_param = var.automatic_choice_penalization;
Location :
Glob_CoefPenalDG
This array stores the penalty coefficients for each boundaries of the mesh (edges in 2-D, faces in 3-D). It is significant only for Interior Penalty Discontinuous formulation.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// to display the penalty coefficients
cout << "Penalty coefficients " << var.Glob_CoefPenalDG << endl;
Location :
mesh_data
This array stores the parameters used to construct the mesh. It is usually a vector of length since only one mesh is used in the simulations. It corresponds to parameters given in the field FileMesh of the data file.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// to display the mesh parameters
cout << "Mesh parameters " << var.mesh_data(0) << endl;
Location :
exit_if_no_boundary_condition
If true, the computation will be stopped is there are faces (or edges in 2-D) on a boundary without boundary conditions. By default, this attributed is true, in order to detect if the user forgot lines ConditionReference in the data file. It can be modified by setting Exit_IfNo_BoundaryCondition in the data file.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// if you do not want to stop the computation because of isolated faces without boundary conditions
var.exit_if_no_boundary_condition = false;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
Location :
var_chrono
It is the stopwatch used in Montjoie to compute the time elapsed during the different stages of the simulation.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// if you want to retrieve a computation time
Real_wp t_mesh = var.var_chrono.GetSeconds("MeshGeneration");
// or display all stopwatches
var.var_chrono.DisplayAll();
Location :
GetNbDof, SetNbDof
Syntax
| int GetNbDof() const |
| void SetNbDof(int N) |
The method GetNbDof returns the total number of degrees of freedom of the solved problem. This number is computed by adding the degrees of freedom for each unknown and optional degrees of freedom due to boundary conditions (or other models). The method SetNbDof changes this number.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// if you want to retrieve the total number of degrees of freedom
int N = var.GetNbDof();
// you want to add a row to the linear system
var.SetNbDof(N+1);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetNbMeshDof
Syntax
| int GetNbMeshDof() const |
| int GetNbMeshDof(int n) const |
This method returns the number of degrees of freedom for the n-th mesh numbering. If no argument is given, it returns the number of degrees for the first mesh numbering.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_SIPG", solver);
// if you want to retrieve the number of dofs for the main unknown
int Nvol = var.GetNbMeshDof();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetNbMeshNumberings
Syntax
| int GetNbMeshNumberings() const |
This method returns the number of mesh numberings.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the number of mesh numberings
int nb_mesh_num = var.GetNbMeshNumberings(); // should be one
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetMeshNumberingBase
Syntax
| const MeshNumbering_Base<Real_wp>& GetMeshNumberingBase(int n = 0) const |
This method gives access to the n-th mesh numbering.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the mesh numbering for the main unknown
const MeshNumbering_Base<Real_wp>& mesh_num = var.GetMeshNumberingBase();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetOffsetDofUnknown
Syntax
| int GetOffsetDofUnknown(int n) const |
This method returns offset_dof_unknown(n) (see details in the description of offset_dof_unknown).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the first row for unknown 2
int N = var.GetOffsetDofUnknown(2);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetOffsetDofCondensed
Syntax
| int GetOffsetDofCondensed(int n) const |
This method returns offset_dof_condensed(n) (see details in the description of offset_dof_condensed).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the first row for unknown 2
int N = var.GetOffsetDofCondensed(2);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetDefaultOrder
Syntax
| int GetDefaultOrder(int r) const |
This method returns the order that will be used for the mesh. It corresponds to the order given when filling OrderGeometry in the data file. If this field is not present, the default order is initialized with the order given in OrderDiscretization.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the order used for the geometry
int r = var.GetDefaultOrder();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
FormulationDG
Syntax
| int FormulationDG() const |
This method returns the attribute dg_formulation.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the formulation used to solve the equation
int dg_form = var.FormulationDG();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
ComputeDFjm1
Syntax
| bool ComputeDFjm1() const |
This method returns the attribute compute_dfjm1.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// jacobian matrices are computed ?
bool dfj_computed = var.ComputeDFjm1();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
FirstOrderFormulation
Syntax
| bool FirstOrderFormulation() const |
This method returns true if a mixed formulation is used. For example, the Helmholtz equation :
is transformed into
which is a mixed formulation of Helmholtz equation. This method is relevant only for continuous formulations. Only some equations have an implementation of a mixed formulation.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
// mixed formulation is used ?
bool mix_form = var.FirstOrderFormulation();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
FirstOrderFormulationDG
Syntax
| bool FirstOrderFormulationDG() const |
This method returns true if only first-order derivatives (in space) appear in the discontinuous Galerkin formulation.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// only first-order derivatives in the formulation ?
bool first_order_deriv = var.FirstOrderFormulationDG();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetFirstOrderFormulation
Syntax
| bool SetFirstOrderFormulation(bool mix = true) |
This method enables (or disables) the use of a mixed formulation (as detailed in FirstOrderFormulation).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;;
// if you want to force a first-order formulation :
var.SetFirstOrderFormulation(true);
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE", solver);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
UseExactIntegrationElement
Syntax
| bool UseExactIntegrationElement() const |
This method returns true if we consider that the used finite element will ensure an exact integration. It is used for some equations, in order to use more efficients formulations. This feature can be used by inserting a line with ExactIntegration in the data file. It is up to the user to be sure that the used finite element ensures an exact integration.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// if the user put a line ExactIntegration = YES, it should return true :
bool exact_integration = var.UseExactIntegrationElement();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetOverIntegration
Syntax
| int GetOverIntegration() const |
This method returns the over-integration used in the simulations. This integer can be modified by inserting a line with ExactIntegration in the data file. Otherwise, it is equal to 0 (no over-integration).
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// is there over-integration ?
// integration or order r+p (where r is the order of the finite element)
int p = var.GetOverIntegration();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetXmin
Syntax
| Real_wp GetXmin() const |
This method returns the minimum of x-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp xmin_d = var.mesh.GetXmin();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetYmin
Syntax
| Real_wp GetYmin() const |
This method returns the minimum of y-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp ymin_d = var.mesh.GetYmin();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetZmin
Syntax
| Real_wp GetZmin() const |
This method returns the minimum of z-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp zmin_d = var.mesh.GetZmin();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetXmax
Syntax
| Real_wp GetXmax() const |
This method returns the maximum of x-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp xmax_d = var.mesh.GetXmax();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetYmax
Syntax
| Real_wp GetYmax() const |
This method returns the maximum of y-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TRIANGLE_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp ymax_d = var.mesh.GetYmax();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetZmax
Syntax
| Real_wp GetZmax() const |
This method returns the maximum of z-coordinates of the physical domain. The physical domain does not include PML layers.
Example :
EllipticProblem<LaplaceEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// bounds of the physical domain
Real_wp xmin = var.GetXmin();
Real_wp xmax = var.GetXmax();
Real_wp ymin = var.GetYmin();
Real_wp ymax = var.GetYmax();
Real_wp zmin = var.GetZmin();
Real_wp zmax = var.GetZmax();
// if you want to know bounds of the computational domain
// (physical domain + PMLs), use mesh
Real_wp zmax_d = var.mesh.GetZmax();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetComputationalDomain
Syntax
| void SetComputationalDomain(Real_wp xmin, Real_wp xmax, Real_wp ymin, Real_wp ymax, Real_wp zmin, Real_wp zmax) |
This method sets the bounds of the physical domain. The physical domain does not include PML layers. The name of the method is misleading since the methods changes the bounds of physical domain (and not the computational domain).
Example :
EllipticProblem<LaplaceEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// if you want to change the bounds of the physical domain
var.SetComputationalDomain(-2.0, 2.0, -2.0, 2.0, -1.0, 1.0);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetOmega, SetOmega
Syntax
| Real_wp GetOmega() const |
| void SetOmega(Real_wp omega) |
The method GetOmega returns the pulsation (which is equal to the frequency multiplied by 2 π) . The method SetOmega sets the pulsation.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// pulsation omega ?
Real_wp omega = var.GetOmega();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetSquareOmega
Syntax
| Real_wp GetSquareOmega() const |
This method returns the square of the pulsation .
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// square of pulsation omega^2 ?
Real_wp omega2 = var.GetSquareOmega();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetMiomega
Syntax
| void GetMiomega(Real_wp& z) const |
| void GetMiomega(Complex_wp& z) const |
This method sets z to - i ω where ω is the pulsation. If z is a real number, it is set to 1.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// -i omega ?
Complex_wp m_iomega; var.GetMiomega(m_iomega);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetMomega2
Syntax
| void GetMomega2(Real_wp& z) const |
| void GetMomega2(Complex_wp& z) const |
This method sets z to - ω2 where ω is the pulsation. If z is a real number, it is set to 1.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// -omega^2 ?
Complex_wp m_omega2; var.GetMomega2(m_omega2);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetFrequency, SetFrequency
Syntax
| Real_wp GetFrequency() const |
| void SetFrequency(Real_wp f) |
The method GetFrequency returns the frequency. The method SetFrequency sets the frequency.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// frequency ?
Real_wp f = var.GetFrequency();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetWaveLengthAdim
Syntax
| Real_wp GetWaveLengthAdim() const |
This method returns the characteristical length. It represents the length of 1 in the mesh. For example if this characteristical length is equal to 1e-9, it means that the units in the mesh are in nanometers (instead of meters). It is modified by adding a line with WavelengthAdim. It is used only if Adimensionalization has been set to YES, and for Helmholtz equations or Maxwell's equations.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// characteristical length
Real_wp L = var.GetWaveLengthAdim();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetDimension
Syntax
| int GetDimension() const |
This method returns the dimension of the solved problem (2 or 3).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// dimension should be three here
int d = var.GetDimension();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetNbComponentsUnkown
Syntax
| int GetNbComponentsUnkown(int n ) const |
This method returns the number of components for an unknown associated with the mesh numbering n . It can be 1 (for a scalar unknown), 2 or 3 (vectorial unknown).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of components for the first mesh numbering ?
int p = var.GetNbComponentsUnknown(0);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblem.cxx
GetNbComponentsGradient
Syntax
| int GetNbComponentsGradient(int n ) const |
This method returns the number of components for the gradient of an unknown associated with the mesh numbering n . It can be 1 (for a scalar unknown), 2 or 3 (vectorial unknown). For edge elements, we consider the curl (instead of the gradient) and for facet elements, the divergence is considered.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of "gradient" components for the first mesh numbering ?
int p = var.GetNbComponentsGradient(0);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblem.cxx
GetNbLocalDof
Syntax
| int GetNbLocalDof(int i ) const |
| int GetNbLocalDof(int i , int n ) const |
This method returns the number of degrees of freedom for the element i . The second argument n is the number of the considered mesh numbering. If not provided, n is equal to zero.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of degrees of freedom for a given element
int i = 3;
int nb_dof = var.GetNbLocalDof(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
GetNbSurfaceDof
Syntax
| int GetNbSurfaceDof(int i ) const |
| int GetNbSurfaceDof(int i , int n ) const |
This method returns the number of degrees of freedom for the surfacic element i . The second argument n is the number of the considered mesh numbering. If not provided, n is equal to zero. This method is relevant for HDG formulation where the surface unknowns λ are discretized with surfacic finite elements.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_HDG", solver);
// number of degrees of freedom for a given face
int i = 3;
int nb_dof = var.GetNbSurfaceDof(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
GetNbDofBoundaries
Syntax
| int GetNbDofBoundaries(int i ) const |
| int GetNbDofBoundaries(int i , int n ) const |
This method returns the number of degrees of freedom for the element i , only degrees of freedom associated with the vertices/edges/faces are counted. We do not count internal degrees of freedom (associated with the inside of the element). The second argument n is the number of the considered mesh numbering. If not provided, n is equal to zero.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of degrees of freedom on the boundaries of an element
int i = 3;
int nb_dof_boundaries = var.GetNbDofBoundaries(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
GetNbPointsQuadratureInside
Syntax
| int GetNbPointsQuadratureInside(int i ) const |
This method returns the number of quadrature points inside the element i .
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of quadrature points for volume integrals of element i
int i = 3;
int nb_quad = var.GetNbPointsQuadratureInside(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
WeightsND
Syntax
| const VectReal_wp& WeightsND(int i ) const |
This method returns the weights associated with quadrature points inside the element i .
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// number of quadrature points for volume integrals of element i
int i = 3;
int nb_quad = var.GetNbPointsQuadratureInside(i);
// associated weights
const VectReal_wp& weights = var.WeightsND(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
InsidePML, ElementInsidePML
Syntax
| bool ElementInsidePML(int i ) const |
| bool InsidePML(int i ) const |
This method returns returns true if the element i is located in PMLs.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// is element i a PML element ?
int i = 3;
bool inside_pml = var.ElementInsidePML(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblemInline.cxx
GetReferenceElementBase
Syntax
| const ElementReference_Base& GetReferenceElementBase(int i ) const |
| const ElementReference_Base& GetReferenceElementBase(int i , int n ) const |
This method returns the finite element associated with the element i . It returns a reference to the base class of the finite element. If you already know the dimension, you can call GetReferenceElement instead. The second argument is optional (if you want to select another mesh numbering).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_DG", solver);
// reference element associated with an element
int i = 3;
const ElementReference_Base& Fb = var.GetReferenceElementBase(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
GetSurfaceElementBase
Syntax
| const ElementReference_Base& GetSurfaceElementBase(int i ) const |
| const ElementReference_Base& GetSurfaceElementBase(int i , int n ) const |
This method returns the finite element associated with the surfacic element i . It returns a reference to the base class of the finite element. If you already know the dimension, you can call GetReferenceElement instead. The second argument is optional (if you want to select another mesh numbering). This method is relevant for HDG formulation (the surfacic elements are associated with surfacic unknowns λ).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_HDG", solver);
// reference element associated with a face
int i = 3;
const ElementReference_Base& Fb = var.GetSurfaceElementBase(i);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemInline.cxx
WriteMesh
Syntax
| void WriteMesh(string file_name) const |
This method writes the mesh in a file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_HDG", solver);
// if you want to write the mesh
var.WriteMesh("test.mesh");
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblemInline.cxx
SetSameNumberPeriodicDofs
Syntax
| void SetSameNumberPeriodicDofs() |
This method forces to use same numbers for periodic dofs. This can also be achieved by inserting a line UseSameDofsForPeriodicCondition = YES in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// if you want to force same numbers for periodic dofs
var.SetSameNumberPeriodicDofs();
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "TETRAHEDRON_CLASSICAL", "LAPLACE_HDG", solver);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblemInline.cxx
InitIndices
Syntax
| void InitIndices(int N) |
This method allocates the arrays storing physical indexes (such as ε, μ for Maxwell's equations). The size of the arrays should be equal to N+1 such that you can use a reference equal to N.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
// we usually put the maximal reference number (Physical Volume in 3-D)
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
// the lines with MateriauDielec or PhysicalMedia must have a number between 1 and N (included)
ReadInputFile("test.ini", var);
// you can continue the computations
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
Location :
GetNbPhysicalIndices
Syntax
| int GetNbPhysicalIndices() |
This method returns the number of physical indices stored in the class. It corresponds to N+1 where N is the argument given when InitIndices has been called.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
// we usually put the maximal reference number (Physical Volume in 3-D)
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
// the lines with MateriauDielec or PhysicalMedia must have a number between 1 and N
ReadInputFile("test.ini", var);
// you can continue the computations
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// if you need to retrieve N+1
int np1 = var.GetNbPhysicalIndices();
Location :
SetIndices
Syntax
| void SetIndices(int ref, const VectString& param) |
This method sets the physical indexes associated with the reference ref. It is the method called when a line MateriauDielec is present in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
// we usually put the maximal reference number (Physical Volume in 3-D)
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
// the lines with MateriauDielec or PhysicalMedia must have a number between 1 and N (included)
ReadInputFile("test.ini", var);
// if you want to add other indexes (not given in the data file)
VectString param(4);
// for Helmholtz equation, we have isotropy rho mu sigma
param(0) = "ISOTROPE"; param(1) = "2.4"; param(2) = "1.5"; param(3) = "0.1";
// it is equivalent to place : MateriauDielec = 4 ISOTROPE 2.4 1.5 0.1
var.SetIndices(4, param);
// you can continue the computations
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
Location :
SetPhysicalIndex
Syntax
| void SetPhysicalIndex(string index_name, int ref, const VectString& param) |
This method sets a single physical index associated with the reference ref. It is the method called when a line PhysicalMedia is present in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
// we usually put the maximal reference number (Physical Volume in 3-D)
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
// the lines with MateriauDielec or PhysicalMedia must have a number between 1 and N (included)
ReadInputFile("test.ini", var);
// if you want to add/modify a single index(not given in the data file)
VectString param(4);
// for Helmholtz equation, we have rho mu sigma
param(0) = "ISOTROPE"; param(1) = "2.4";
// it is equivalent to place : PhysicalMedia = rho 4 ISOTROPE 2.4
var.SetPhysicalIndex("rho", 4, param);
// you can continue the computations
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
Location :
IsVaryingMedia
Syntax
| bool IsVaryingMedia(int ref) const |
| bool IsVaryingMedia(int m, int ref) const |
This method returns true if one of the physical index of reference ref is variable. In the second syntax, (which is used only for unsteady simulations with discontinuous Galerkin), the method returns true if the physical index associated with the unknown m is variable (mass and/or damping terms) for the reference ref.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
ReadInputFile("test.ini", var);
// you can continue the computations
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// variable index for reference 5 ?
bool variable = var.IsVaryingMedia(5);
Location :
GetPhysicalIndexName
Syntax
| string GetPhysicalIndexName(int m) const |
This method returns the name of the m-th physical index. It depends on the solved equation. For example, it will return "rho" for Helmholtz equation and m = 0.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ");
// then you can read the data file
ReadInputFile("test.ini", var);
// name of the physical index 1 ?
string name = var.GetPhysicalIndexName(1);
Location :
GetCoefficientPenaltyStiffness
Syntax
| Real_wp GetCoefficientPenaltyStiffness(int ref) const |
This method returns the physical coefficient associated with reference ref. This coefficient will be used for the penalty terms of the Interior Penalty Discontinuous Galerkin method. For Helmholtz equation, it will correspond to the amplitude of μ.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ_SIPG");
// then you can read the data file
ReadInputFile("test.ini", var);
// coefficient for penalty terms
Real_wp mu_coef = var.GetCoefficientPenaltyStiffness(5);
Location :
GetVelocityOnElements
Syntax
| void GetVelocityOnElements(VectReal_wp& velocity, Mesh<Dimension>& mesh) |
This method fills the array velocity with the velocities for each element of the mesh.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ_SIPG");
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh is constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// velocities for all elements
VectReal_wp velocity;
var.GetVelocityOnElements(velocity, var.mesh);
Location :
GetVelocityOfMedia
Syntax
| Real_wp GetVelocityOfMedia(int ref) |
This method returns the velocity of the physical media (corresponding to elements whose reference is equal to ref).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ_SIPG");
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh is constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// velocities for a given reference
Real_wp c var.GetVelocityOfMedia(1);
Location :
GetVelocityOfInfinity
Syntax
| void GetVelocityOfInfinity() |
This method returns the velocity associated with the infinity. This quantity is used for absorbing boundary conditions. It is correctly computed if the user has inserted a line ReferenceInfinity in the data file, such that the physical indexes are known at the infinity.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ_SIPG");
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh is constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// velocity for reference 5 ?
Real_wp c = var.GetVelocityOfMedia(5);
// and for the media at infinity ?
Real_wp c_inf = var.GetVelocityOfInfinity();
Location :
CopyInputData
Syntax
| void CopyInputData(const VarProblem_Base& var) |
This method copies input parameters from another similar object.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var, var_bis;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("HELMHOLTZ_SIPG");
// then you can read the data file (input parameters are read from a file)
ReadInputFile("test.ini", var);
// you can copy input parameters to object var_bis
var_bis.CopyInputData(var);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
IsSymmetricProblem
Syntax
| bool IsSymmetricProblem(bool eigen=false) const |
This method returns true if the finite element matrix is symmetric. The second argument is optional. If eigen is equal to true, we ask if the eigenproblem is symmetric (with a positive definite mass matrix).
Example :
EllipticProblem<LaplaceEquation<Dimension3> > var;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("LAPLACE");
// then you can read the data file (input parameters are read from a file)
ReadInputFile("test.ini", var);
// symmetric finite element matrix ?
bool sym = var.IsSymmetricProblem();
Location :
IsSymmetricMassMatrix
Syntax
| bool IsSymmetricMassMatrix() const |
This method returns true if the mass matrix is symmetric.
Example :
EllipticProblem<LaplaceEquation<Dimension3> > var;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("LAPLACE");
// then you can read the data file (input parameters are read from a file)
ReadInputFile("test.ini", var);
// symmetric mass matrix ?
bool sym = var.IsSymmetricMassMatrix();
Location :
IsComplexProblem
Syntax
| bool IsComplexProblem() const |
This method returns true if the solved equation has to be solved with complex numbers.
Example :
EllipticProblem<LaplaceEquation<Dimension3> > var;
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation("LAPLACE");
// then you can read the data file (input parameters are read from a file)
ReadInputFile("test.ini", var);
// complex numbers ? LaplaceEquation is solved with real numbers => we should get false
bool cplx = var.IsComplexProblem();
Location :
ComputeMeshAndFiniteElement
Syntax
| void ComputeMeshAndFiniteElement(string name_finite_element) |
| void ComputeMeshAndFiniteElement(string name_finite_element, bool split_mesh) |
This method computes the mesh and constructs the finite elements. The name of the main finite element (to use for the main unknown) is given as argument. It corresponds to the line TypeElement of the data file. The second argument is optional and is meaningful in parallel. If true, the mesh is distributed between the different processors.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarGeometryProblem.cxx
PerformOtherInitializations
Syntax
| void PerformOtherInitializations() |
This method performs other initializations (if there are specific models to initialize or specific boundary conditions). This method is called after constructing the mesh and finite elements.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
Location :
SetTypeEquation
Syntax
| void SetTypeEquation(string name_finite_element) |
This method sets the type of equation to solve. The name of the equation gives also the formulation used to solve it (discontinuous, hdg, etc). This method is called just after InitIndices such that the array is correctly filled.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetThresholdMatrix
Syntax
| void GetThresholdMatrix() const |
This method returns the threshold used to drop values in the finite element matrix. All values below this threshold (in magnitude) are dropped. It corresponds to the value given by the field ThresholdMatrix in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Real_wp, Symmetric, ArrayRowSymSparse> A;
// which threshold is set in the data file ?
cout << "Threshold for matrix = " << var.GetThresholdMatrix() << endl;
var.AddMatrixWithBC(A, nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
SetThresholdMatrix
Syntax
| void SetThresholdMatrix(Real_wp eps) |
This method sets the threshold used to drop values in the finite element matrix. All values below this threshold (in magnitude) are dropped. It corresponds to the value given by the field ThresholdMatrix in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Real_wp, Symmetric, ArrayRowSymSparse> A;
// if you want a sparser matrix, you can drop small values
// (if the threshold is too large, the solution will be less accurate
var.SetThresholdMatrix(1e-12);
var.AddMatrixWithBC(A, nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNbElt
Syntax
| int GetNbElt() const |
This method returns the number of elements of the mesh (number of faces in 2-D, number of volumes in 3-D).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
// number of elements
int nb_elt = var.GetNbElt();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNbRows
Syntax
| int GetNbRows() const |
This method returns the number of rows of the finite element matrix.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
// size of matrix
int nb_rows = var.GetNbRows();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetPrintLevel
Syntax
| int GetPrintLevel() const |
This method returns the verbosity level used in Montjoie. Higher values induces more informations to be displayed during the simulation. A print level negative or null implies that Montjoie is silencious (no messages are displayed). It corresponds to the field PrintLevel in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// print level ?
int print_level = var.GetPrintLevel();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
ComputeElementaryMatrix
Syntax
| void ComputeElementaryMatrix(int i, IVect& num_ddl, VirtualMatrix& A, CondensationBlockSolver_Base& solver, const GlobalGenericMatrix& nat_mat) const |
This method computes the elementary matrix of a given element. Actually, this method is overloaded for each equation solved in Montjoie. If you want to compute the global finite element matrix, AddMatrixWithBC should be called.
Parameters
- i (in)
- element number
- num_ddl (out)
- global row numbers
- A (out)
- elementary matrix
- solver (out)
- solver handling static condensation
- nat_mat (in)
- mass, damping and stiffness coefficients
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat;
// if you need only an elementary matrix
// (for the global matrix, call AddMatrixWithBC)
int num_elem = 5;
IVect num_row; Matrix<Complex_wp> mat_elem;
CondensationBlockSolver_Base<Complex_wp> cond_solver;
var.ComputeElementaryMatrix(num_elem, num_row, mat_elem, cond_solver, nat_mat);
Location :
GetInternalNodesElement
Syntax
| void GetInternalNodesElement(int i, int nb_dof_loc, int& nb_dof_edges, int& nb_dof_int, IVect& intern_node) const |
This method is used to know which rows of the elementary matrix will be condensed.
Parameters
- i (in)
- element number
- nb_dof_loc (in)
- number of degrees of freedom of element i
- nb_dof_edges (out)
- number of degrees of freedom that cannot be eliminated
- nb_dof_int (out)
- number of degrees of freedom that will be condensed
- intern_node (in)
- If intern_node(i) is nonnegative, it is the local number among rows that are conserved after condensation. If intern_node(i) is negative, -intern_node(i)-1 is the local number among rows that are eliminated after condensation.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat;
// if you need only an elementary matrix
// (for the global matrix, call AddMatrixWithBC)
int num_elem = 5;
IVect num_row; Matrix<Complex_wp> mat_elem;
CondensationBlockSolver_Base<Complex_wp> cond_solver;
var.ComputeElementaryMatrix(num_elem, num_row, mat_elem, cond_solver, nat_mat);
// if you want to know which rows can be eliminated
int nb_dof_edges, nb_dof_inside; Vector<int> intern_node;
var.GetInternalNodesElement(i, mat_elem.GetM(), nb_dof_edges, nb_dof_inside, intern_node);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNewCondensationSolver
Syntax
| CondensationBlockSolver_Base<Real_wp>* GetNewCondensationSolver(Real_wp) |
| CondensationBlockSolver_Base<Complex_wp>* GetNewCondensationSolver(Complex_wp) |
This method constructs a new object handling static condensation. This new object is suited for the solved equation.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat;
// if you want an adapted condensation solver
CondensationBlockSolver_Base<Complex_wp>* cond_solver;
cond_solver = var.GetNewCondensationSolver(Complex_wp(0));
// if you need only an elementary matrix
// (for the global matrix, call AddMatrixWithBC)
int num_elem = 5;
IVect num_row; Matrix<Complex_wp> mat_elem;
var.ComputeElementaryMatrix(num_elem, num_row, mat_elem, *cond_solver, nat_mat);
// the created object must be deleted after use
delete cond_solver;
Location :
UseMatrixFreeAlgorithm
Syntax
| bool UseMatrixFreeAlgorithm() const |
This method returns true if the finite element matrix will not be stored (if an iterative matrix is constructed).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
bool matrix_stored = var.UseMatrixFreeAlgorithm(); // matrix will be stored ?
// computation of the iterative matrix
FemMatrixFreeClass_Base<Complex_wp>* A = var.GetNewIterativeMatrix(Complex_wp(0));
GlobalGenericMatrix<Complex_wp> nat_mat;
var.AddMatrixWithBC(*A, nat_mat);
delete A;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
IsSymmetricGlobalMatrix
Syntax
| bool IsSymmetricGlobalMatrix() const |
This method returns true if the global finite element matrix is symmetric.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
bool sym = var.IsSymmetricGlobalMatrix(); // matrix is symmetric ?
GlobalGenericMatrix<Complex_wp> nat_mat;
if (sym)
{
DistributedMatrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
}
else
{
DistributedMatrix<Complex_wp, General, ArrayRowSparse> A;
var.AddMatrixWithBC(A, nat_mat);
}
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetStorageFiniteElementMatrix
Syntax
| int GetStorageFiniteElementMatrix() const |
This method returns the storage used for the computation of the iterative matrix. The following storages are possible :
- MATRIX_AUTO_STORAGE : Montjoie selects automatically if the matrix is stored or not
- MATRIX_STORED : the iterative matrix is stored
- MATRIX_FREE : the iterative matrix is not stored
This storage is chosen by inserting a line with the field ExplicitMatrixFEM in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// storage for the iterative matrix
int storage = var.GetStorageFiniteElementMatrix();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetStorageFiniteElementMatrix
Syntax
| void SetStorageFiniteElementMatrix(int type) |
This method sets the storage used for the computation of the iterative matrix. The following storages are possible :
- MATRIX_AUTO_STORAGE : Montjoie selects automatically if the matrix is stored or not
- MATRIX_STORED : the iterative matrix is stored
- MATRIX_FREE : the iterative matrix is not stored
This storage can also be chosen by inserting a line with the field ExplicitMatrixFEM in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// if you want to change the storage of the iterative matrix
var.SetStorageFiniteElementMatrix(var.MATRIX_STORED);
// computation of the iterative matrix
FemMatrixFreeClass_Base<Complex_wp>* A = var.GetNewIterativeMatrix(Complex_wp(0));
GlobalGenericMatrix<Complex_wp> nat_mat;
var.AddMatrixWithBC(*A, nat_mat);
delete A;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetSymmetricElementaryMatrix
Syntax
| void SetSymmetricElementaryMatrix(bool sym=true) |
This method can be used to modify the type of elementary matrix.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// if you want to change the type of symmetry for the elementary matrix
// it is not needed to set it, since the correct type is usually automatically selected
var.SetSymmetricElementaryMatrix(false); // unsymmetric elementary matrix
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetLeafStaticCondensation
Syntax
| void SetLeafStaticCondensation(bool condensed=true) |
This method is used to tell Montjoie that the static condensation has to been performed. If condensed is true (and if static condensation has been enabled), the condensed matrix will be computed if AddMatrixWithBC is called, otherwise the non-condensed matrix is computed. This method does not enable or disable static condensation, it is done by inserting a line StaticCondensation in the data file. Thanks to the method SetLeafStaticCondensation, the user can compute the non-condensed matrix even though the static condensation has been enabled (to compute efficiently the solution).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to tell that we want to compute the non-condensed matrix
var.SetLeafStaticCondensation(false);
// computation of the matrix
GlobalGenericMatrix<Complex_wp> nat_mat;
DistributedMatrix<Complex_wp, General, ArrayRowSparse> A;
var.AddMatrixWithBC(A, nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetLeafStaticCondensation
Syntax
| bool GetLeafStaticCondensation() const |
This method returns true if the static condensation has to been effectively performed. More details are given in the description of SetLeafStaticCondensation.
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
LightStaticCondensation
Syntax
| bool LightStaticCondensation() const |
This method returns true if a light static condensation is enabled. A light static condensation consists of removing discontinuous unknowns (labelled as vectorial unknowns) whereas continuous unknowns (labelled as scalar unknowns) are conserved. This method makes sense only for a continuous formulation of the equation. Internal degrees of freedom are not eliminated as done by a regular static condensation. A light static condensation is enabled if the user inserts the following line in the data file :
TypeCondensation = Light
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// light static condensation ?
bool light = var.LightStaticCondensation();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
GetSymmetrizationUse
Syntax
| bool GetSymmetrizationUse() const |
This method returns true if a symmetrization is used (if possible). For example, Helmholtz equation (in the mixed formulation) given as
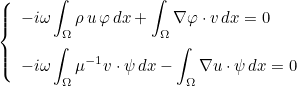
can be symmetrized by multiplying the second equation by -1. With this modification, the finite element matrix is symmetric. This symmetrization is possible for specific equations.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// use of a symmetrization ?
bool use_sym = var.GetSymmetrizationUse();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetSymmetrizationUse
Syntax
| void SetSymmetrizationUse(bool sym=true) const |
This method can be used if the user wants to use a symmetrization (if possible). For example, Helmholtz equation (in the mixed formulation) given as
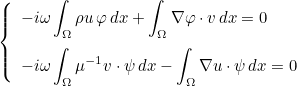
can be symmetrized by multiplying the second equation by -1. With this modification, the finite element matrix is symmetric. This symmetrization is possible for specific equations. It is advised to check that the finite element matrix will be symmetric by calling IsSymmetricProblem.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// we want to symmetrize the matrix if possible
var.SetSymmetrizationUse();
// checking that the matrix will be symmetric
bool sym = var.IsSymmetricProblem();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetHomogeneousDirichlet
Syntax
| void SetHomogeneousDirichlet(bool hg_dir) const |
This method informs Montjoie that all the Dirichlet conditions are homogeneous (i.e. u = 0) if hg_dir is true. If a Dirichlet condition is hetereogeneous (i.e. u = f), hg_dir should be set to false.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you are sure that all Dirichlet conditions are homogeneous (u = 0)
// then you can say it :
var.SetHomogeneousDirichlet(true);
// it will save time for the computation of the solution
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
IsHomogeneousDirichlet
Syntax
| bool IsHomogeneousDirichlet() const |
This method returns true if only Homogeneous Dirichlet conditions (i.e. u = 0) are present.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you are sure that all Dirichlet conditions are homogeneous (u = 0)
// then you can say it :
var.SetHomogeneousDirichlet(true);
// it will save time for the computation of the solution
// then IsHomogeneousDirichlet should return true
bool hg = var.IsHomogeneousDirichlet();
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
SetPrintLevel
Syntax
| void SetPrintLevel(int level) const |
This method sets the verbosity level used in Montjoie. Higher values induces more informations to be displayed during the simulation. A print level negative or null implies that Montjoie is silencious (no messages are displayed). It corresponds to the field PrintLevel in the data file.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// print level ?
int print_level = var.GetPrintLevel();
// if you want to change it (for example to keep Montjoie silent for a specific computation
var.SetPrintLevel(0);
// and you can get back to the previous print level
var.SetPrintLevel(print_level);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBaseInline.cxx
AddMatrixWithBC
Syntax
| void AddMatrixWithBC( | Matrix& A, const GlobalGenericMatrix& nat_mat, int offset_row = 0, int offset_col = 0, |
| CondensationBlockSolver_Fem* solver = NULL, bool diag_matrix = false) const |
This method computes the finite element matrix (with boundary terms). It works if A is an iterative matrix or if A is a distributed matrix. In this last case, the finite element matrix is added to the previously matrix given as argument. The object nat_mat stores the mass coefficient α, damping coefficient β, stiffness coefficient γ such that the following matrix is computed :

For time-harmonic equations, these coefficients are usually set to one. For unsteady equations, these coefficients depend on the used time scheme.
Parameters
- A (inout)
- finite element matrix
- nat_mat (in)
- mass, damping and stiffness coefficients
- offset_row (optional)
- offset for row numbers
- offset_col (optional)
- offset for column numbers
- solver (optional)
- solver handling static condensation
- diag_matrix (optional)
- true if only the diagonal of the matrix has to be computed
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixWithBC
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat); // A is a sparse matrix => it is stored
// if you only need an iterative matrix (the matrix is not necessarily stored)
// ie only the matrix-vector product is needed
FemMatrixFreeClass_Base<Complex_wp>* Aiter = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Aiter, nat_mat);
delete Aiter;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
AddMatrixFEM
Syntax
| void AddMatrixFEM( | Matrix& A, const GlobalGenericMatrix& nat_mat, int offset_row = 0, int offset_col = 0, |
| CondensationBlockSolver_Fem* solver = NULL, bool diag_matrix = false) const |
This method computes the finite element matrix (without boundary terms). It works if A is an iterative matrix or if A is a distributed matrix. In this last case, the finite element matrix is added to the previously matrix given as argument. The object nat_mat stores the mass coefficient α, damping coefficient β, stiffness coefficient γ such that the following matrix is computed :
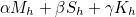
For time-harmonic equations, these coefficients are usually set to one. For unsteady equations, these coefficients depend on the used time scheme.
Parameters
- A (inout)
- finite element matrix
- nat_mat (in)
- mass, damping and stiffness coefficients
- offset_row (optional)
- offset for row numbers
- offset_col (optional)
- offset for column numbers
- solver (optional)
- solver handling static condensation
- diag_matrix (optional)
- true if only the diagonal of the matrix has to be computed
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can call AddMatrixFEM
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
Matrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixFEM(A, nat_mat); // A is a sparse matrix => it is stored
// here only volume integrals are computed (no boundary conditions)
// if you only need an iterative matrix (the matrix is not necessarily stored)
// ie only the matrix-vector product is needed
FemMatrixFreeClass_Base<Complex_wp>* Aiter = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixFEM(*Aiter, nat_mat);
delete Aiter;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
ComputeDiagonalMatrix
Syntax
| void ComputeDiagonalMatrix( | Vector& diagonal, const GlobalGenericMatrix& nat_mat, bool assemble = true); |
| void ComputeDiagonalMatrix( | Vector& diagonal, Matrix& A, const GlobalGenericMatrix& nat_mat, bool assemble = true); |
This method computes the diagonal of the finite element matrix. In the first syntax, only mass, damping and stiffness coefficients are provided. In the second syntax, the computed matrix is provided (iterative or distributed).
Parameters
- diagonal (out)
- diagonal of the matrix
- A (optional)
- finite element matrix previously computed
- nat_mat (in)
- mass, damping and stiffness coefficients
- assemble (optional)
- if true, the diagonal is assembled (between processors)
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// once var is constructed, you can compute the diagonal of the matrix
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to set coefficients alpha, beta and gamma
// By default, alpha = beta = gamma = 1
VectComplex_wp diagonal;
var.ComputeDiagonalMatrix(diagonal, nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
IsSymmetricElementaryMatrix
Syntax
| bool IsSymmetricElementaryMatrix( | const GlobalGenericMatrix& nat_mat) const; |
This method returns true if the elementary matrix (with coefficients given in nat_mat) is symmetric. This method is called to select the correct type of elementary matrix when the matrix is computed with AddMatrixWithBC.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
// is the elementary matrix symmetric ?
GlobalGenericMatrix<Complex_wp> nat_mat;
nat_mat.SetCoefDamping(Complex_wp(0)); // you can change some coefficients
bool sym = var.IsSymmetricElementaryMatrix(nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
IsDiagonalElementaryMatrix
Syntax
| bool IsDiagonalElementaryMatrix( | const GlobalGenericMatrix& nat_mat) const; |
This method returns true if the elementary matrix (with coefficients given in nat_mat) is symmetric. This method is called to select the correct type of elementary matrix when the matrix is computed with AddMatrixWithBC. For example, it will return true if you ask to compute the mass matrix with mass-lumped elements (for most of equations).
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
// is the elementary matrix diagonal ?
GlobalGenericMatrix<Complex_wp> nat_mat;
nat_mat.SetCoefDamping(Complex_wp(0)); // you can change some coefficients
nat_mat.SetCoefStiffness(Complex_wp(0));
// alpha = 1, beta = gamma = 0 => mass matrix is asked
bool diag = var.IsDiagonalElementaryMatrix(nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
IsSparseElementaryMatrix
Syntax
| bool IsSparseElementaryMatrix( | const GlobalGenericMatrix& nat_mat) const; |
This method returns true if the elementary matrix (with coefficients given in nat_mat) is sparse. This method is called to select the correct type of elementary matrix when the matrix is computed with AddMatrixWithBC.
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
// is the elementary matrix sparse ?
GlobalGenericMatrix<Complex_wp> nat_mat;
nat_mat.SetCoefDamping(Complex_wp(0)); // you can change some coefficients
nat_mat.SetCoefStiffness(Complex_wp(0));
// alpha = 1, beta = gamma = 0 => mass matrix is asked
bool sparse = var.IsSparseElementaryMatrix(nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetStaticCondensedRows
Syntax
| void GetStaticCondensedRows( | IVect& IndexCondensedRows, IVect& global_row, IVect& overlap_row, IVect& overlap_proc, |
| int& nb_scalar_dof, int& nb_global_dof, IVect& sharing_procs, Vector<IVect>& sharing_rows) const |
This method computes the row numbers of degrees of freedom after a static condensation. It is used to construct a distributed matrix with only condensed degrees of freedom (hence, the matrix has a small size).
Parameters
- IndexCondensedRows (inout)
- IndexCondensedRows(i) is equal to -1 if the dof is eliminated, and to index if the dof is kept. The condensed matrix will be a smaller matrix using "index" as row/column numbers.
- global_row (out)
- global row numbers of the condensed matrix
- overlap_row (out)
- dofs that are owned by another processor
- overlap_proc (out)
- processor that owns the overlapped dofs
- nb_scalar_dof (out)
- number of dofs per unknown for the condensed matrix
- nb_global_dof (out)
- global size of the condensed matrix
- sharing_procs (out)
- numbers of processors that share dofs with current processor
- sharing_rows (out)
- row numbers of shared dofs
Example :
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to construct a distributed matrix with condensed dofs :
IVect IndexCondensedRows, global_row, overlap_row, overlap_proc, sharing_procs;
int nb_scalar_dof, nb_global_dof; Vector<IVect> sharing_rows;
var.GetStaticCondensedRows(IndexCondensedRows, global_row, overlap_row, overlap_proc,
nb_scalar_dof, nb_global_dof, sharing_procs, sharing_rows);
int nb_u = 1;
if (var.GetNbMeshNumberings() == 1)
nb_u = var.nb_unknowns_scal;
DistributedMatrix<Complex_wp, General, ArrayRowSparse> A;
A.Init(nb_global_dof, global_row, overlap_row, overlap_proc, nb_scalar_dof, nb_u,
sharing_procs, sharing_rows, var.comm_group_mode);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/DistributedProblem.cxx
AddElementaryFluxesDG
Syntax
| void AddElementaryFluxesDG( | Matrix& A, const GlobalGenericMatrix& nat_mat, int offset_row = 0, int offset_col = 0) |
This method adds to the given matrix A the terms due to numerical fluxes (for a Discontinuous Galerkin formulation). It is called by AddMatrixWithBC.
Parameters
- A (inout)
- matrix to modify
- nat_mat (in)
- mass, damping and stiffness coefficients
- offset_row (optional)
- offset for row numbers
- offset_col (optional)
- offset for column numbers
Example :
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// matrix with only numerical fluxes
GlobalGenericMatrix<Complex_wp> nat_mat;
DistributedMatrix<Complex_wp, General, ArrayRowSparse> A;
A.Reallocate(var.GetNbDof(), var.GetNbDof());
var.AddElementaryFluxesDG(A, nat_mat);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
UpdateShiftAdimensionalization
Syntax
| void UpdateShiftAdimensionalization( | T& sr, T& si) |
This method updates the shifts (for the computation of eigenvalues) because of adimensionalization. The method modifies the shifts such that they are adimensionalized. This methods modifies the shifts only if there is a line Adimensionalization = YES in the data file.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// physical shift (square of pulsation) for second-order formulation
Real_wp freq = 4000; // frequency in Hz
Real_wp omega = 2*pi*freq;
Real_wp sr = square(omega), si = 0;
// we want to know adimensionalized shifts (which correspond to the computed finite element matrix which is adimensionalized)
var.UpdateShiftAdimensionalization(sr, si);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
UpdateEigenvaluesAdimensionalization
Syntax
| void UpdateEigenvaluesAdimensionalization( | Vector& Lr, Vector& Li, Matrix& V) |
This method updates the eigenvalues (stored in Lr and Li) and the eigenvectors (stored in V) . The obtained eigenvalues are the physical ones. This methods modifies the eigenvalues only if there is a line Adimensionalization = YES in the data file.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// physical shift (square of pulsation) for second-order formulation
Real_wp freq = 4000; // frequency in Hz
Real_wp omega = 2*pi*freq;
Real_wp sr = square(omega), si = 0;
// we want to know adimensionalized shifts (which correspond to the computed finite element matrix which is adimensionalized)
var.UpdateShiftAdimensionalization(sr, si);
DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse> Mh, Kh;
GlobalGenericMatrix<Real_wp> nat_mat;
nat_mat.SetCoefDamping(0.0); nat_mat.SetCoefStiffness(0.0);
var.AddMatrixWithBC(Mh, nat_mat);
nat_mat.SetCoefMass(0.0); nat_mat.SetCoefStiffness(1.0);
var.AddMatrixWithBC(Kh, nat_mat);
// we compute eigenvalues and eigenvectors
SparseEigenProblem<Real_wp, DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse>,
DistributedMatrix<Real_wp, Symmetric, ArrayRowSymSparse> > eigen_solver;
eigen_solver.InitMatrix(Kh, Mh);
eigen_solver.SetTypeSpectrum(eigen_solver.CENTERED_EIGENVALUES, sr, eigen_solver.SORTED_MODULUS);
VectReal_wp Lr, Li; Matrix<Real_wp, General, ColMajor> V;
GetEigenvaluesEigenvectors(eigen_solver, Lr, Li, V);
// adimensionalized eigenvalues are computed
// then we get back to physical eigenvalues
var.UpdateEigenvaluesAdimensionalization(Lr, Li, V);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
FindIntervalDofSignSymmetry
Syntax
| void FindIntervalDofSignSymmetry( | int& i0, int& i1, int& j0, int& j1) const |
This method is relevant only if a symmetrization is enabled (see SetSymmetrizationUse). It provides the rows that are multiplied by -1 (to obtain a symmetric matrix). The rows between i0 and i1 (i1 being exlcuded) and the rows between j0 and j1 are multiplied by -1.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// rows modified because of symmetrization ? (mixed formulation)
int i0=0, i1=0, j0=0, j1=0;
var.FindIntervalDofSignSymmetry(i0, i1, j0, j1);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
ModifySourceSymmetry
Syntax
| void ModifySourceSymmetry( | Vector& rhs) const |
| void ModifySourceSymmetry( | Matrix& rhs) const |
This method is relevant only if a symmetrization is enabled (see SetSymmetrizationUse). It modifies the right hand side by multiplying some rows by -1 (some rows of the finite element matrix have been multiplied by -1 to obtain a symmetric matrix). A matrix can be provided in the case of multiplie right hand sides.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// filling a right hand side
VectComplex_wp rhs(var.GetNbDof()); rhs.FillRand();
// rows affected by the symmetrization are multiplied by -1
var.ModifySourceSymmetry(rhs);
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNewIterativeMatrix
Syntax
| FemMatrixFreeClass_Base<T>* GetNewIterativeMatrix( | T& s) const |
This method constructs a new object (representing the iterative matrix) and returns the address of the created object. The object is usually an instance of FemMatrixFreeClass (that depends on the solved equation). The method GetNewIterativeMatrix returns a pointer of the base class FemMatrixFreeClass_Base such that it can be used in generic functions.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNewLinearSolver
Syntax
| All_LinearSolver* GetNewLinearSolver() const |
This method constructs a new object (representing the linear solver) and returns the address of the created object. This solver can be used to compute the solution of a linear system with the finite element matrix.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// creation of the linear solver
All_LinearSolver* solver = var.GetNewLinearSolver();
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// and solve the linear system A x = b
VectComplex_wp b(var.GetNbDof()), x; b.FillRand();
x = b; solver->ComputeSolution(x);
// when you no longer need the solver, you can release the memory
delete solver;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
GetNewPreconditioning
Syntax
| All_Preconditioner_Base<T>* GetNewPreconditioning(T) |
This method constructs a new object (representing the preconditioning) and returns the address of the created object. This preconditioning can be used to compute efficiently the solution of a linear system with the finite element matrix.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
FemMatrixFreeClass_Base<Complex_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// creation of the preconditioning
All_Preconditioner_Base<Complex_wp> prec = var.GetNewPreconditioning();
// to apply the preconditioning to a vector
VectComplex_wp r(var.GetNbDof()), z(var.GetNbDof()); r.FillRand();
prec->Solve(*Ah, r, z); // z = M^{-1} r
// when you no longer need the preconditioning, you can release the memory
delete prec;
Location :
Harmonic/VarProblemBase.hxx
Harmonic/VarProblemBase.cxx
ComputeElementaryMatrix
Syntax
| void ComputeElementaryMatrix( | int i, IVect& num_ddl, VirtualMatrix& A, const GlobalGenericMatrix& nat_mat, |
| const EllipticProblem& var, const ElementReference& Fb) const |
This generic function computes the elementary matrix of a given element. It is implemented if all finite elements are scalar. It is also implemented if all finite elements are 2-D edge elements. This function has to be distinguished from the method ComputeElementaryMatrix of the class EllipticProblem. Most of the times, the method ComputeElementaryMatrix will call the generic function ComputeElementaryMatrix (except for specific equations).
Parameters
- i (in)
- element number
- num_ddl (out)
- global row numbers
- A (out)
- elementary matrix
- nat_mat (in)
- mass, damping and stiffness coefficients
- var (in)
- object describing the problem to solve
- Fb (in)
- finite element associated with the element i
Example :
// to define your own equation
class MyEquation : GenericEquation_Base<Complex_wp>
{
public:
typedef Dimension3 Dimension;
static const bool FirstOrderFormulation = true;
enum {nb_unknowns = 3, nb_unknowns_hdg=0,
nb_components_en = 1, nb_components_hn = 1,
nb_unknowns_scal = 3, nb_unknowns_vec = 0};
static inline bool SymmetricGlobalMatrix() { return false; }
static inline bool SymmetricElementaryMatrix() { return false; }
// other functions ( such as GetTensorMass, GetGradPhiTensor, etc)
// need to be overloaded
};
// in the specialization of EllipticProblem
// you can call the generic function ComputeElementaryMatrix
template<>
class EllipticProblem<MyEquation>
: public VarHarmonic <MyEquation>
{
public :
void ComputeElementaryMatrix(int i, IVect& num_dof, VirtualMatrix<Complex_wp>& mat_elem,
CondensationBlockSolver_Base<Complex_wp>&,
const GlobalGenericMatrix<Complex_wp>& nat_mat)
{
// we call generic function
Montjoie::ComputeElementaryMatrix(i, num_dof, mat_elem, nat_mat, *this, this->GetReferenceElementH1(i));
}
};
Location :
Computation/ElementaryMatrixH1.hxx
Computation/ElementaryMatrixH1.cxx
AddElementaryFluxesDG
Syntax
| void AddElementaryFluxesDG(VirtualMatrix& A, const GlobalGenericMatrix& nat_mat, const EllipticProblem& var, int offset_row, int offset_col) const |
This generic function computes the boundary terms associated with numerical fluxes (for a Discontinuous Galerkin formulation) and adds them to a given matrix. It is implemented if all finite elements are scalar. This function has to be distinguished from the method AddElementaryFluxesDG of the class EllipticProblem. Most of the times, the method AddElementaryFluxesDG will call the generic function AddElementaryFluxesDG (except for specific equations).
Parameters
- A (out)
- elementary matrix
- nat_mat (in)
- mass, damping and stiffness coefficients
- var (in)
- object describing the problem to solve
- offset_row (in)
- offset for row numbers
- offset_col (in)
- offset for column numbers
Example :
// to define your own equation
class MyEquation : GenericEquation_Base<Complex_wp>
{
public:
typedef Dimension3 Dimension;
static const bool FirstOrderFormulation = true;
enum {nb_unknowns = 3, nb_unknowns_hdg=0,
nb_components_en = 1, nb_components_hn = 1,
nb_unknowns_scal = 3, nb_unknowns_vec = 0};
static inline bool SymmetricGlobalMatrix() { return false; }
static inline bool SymmetricElementaryMatrix() { return false; }
// other functions ( such as GetTensorMass, GetGradPhiTensor, etc)
// need to be overloaded
};
// in the specialization of EllipticProblem
// you can call the generic function ComputeElementaryMatrix and ElementaryFluxesDG
template<>
class EllipticProblem<MyEquation>
: public VarHarmonic <MyEquation>
{
public :
void ComputeElementaryMatrix(int i, IVect& num_dof, VirtualMatrix<Complex_wp>& mat_elem,
CondensationBlockSolver_Base<Complex_wp>&,
const GlobalGenericMatrix<Complex_wp>& nat_mat)
{
// we call generic function
Montjoie::ComputeElementaryMatrix(i, num_dof, mat_elem, nat_mat, *this, this->GetReferenceElementH1(i));
}
void AddElementaryFluxesDG(VirtualMatrix<Complex_wp<& mat_sp,
const GlobalGenericMatrix<Complex_wp>& nat_mat,
int offset_row, int offset_col)
{
Montjoie::AddElementaryFluxesDG(mat_sp, nat_mat, *this, offset_row, offset_col);
}
};
Location :
Computation/ElementaryMatrixH1.hxx
Computation/ElementaryMatrixH1.cxx
mat_boundary_sym, mat_boundary_unsym
The attribute mat_boundary_sym stores the terms due to boundary conditions (or other models) in the case where the finite element matrix is symmetric. If the matrix is unsymmetric, the attribute mat_boundary_unsym is used.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// you can write terms due to boundary conditions
Ah->mat_boundary_sym.WriteText("mat_boundary.dat");
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Computation/FemMatrixFreeClass.hxx
matCSR_boundary_sym, matCSR_boundary_unsym
The attribute matCSR_boundary_sym stores the terms due to boundary conditions (or other models) in the case where the finite element matrix is symmetric. If the matrix is unsymmetric, the attribute matCSR_boundary_unsym is used. These matrices are constructed if the method CompressMatrix has been called previously.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// matrices are compressed (use of CSR storage)
Ah->CompressMatrix();
// you can write terms due to boundary conditions
Ah->matCSR_boundary_sym.WriteText("mat_boundary.dat");
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Computation/FemMatrixFreeClass.hxx
mat_iterative_sym, mat_iterative_unsym
The attribute mat_iterative_sym stores the finite element matrix if it is stored (and symmetric). If the matrix is unsymmetric, the attribute mat_iterative_unsym is used. To force the storage of the matrix, you can insert a line ExplicitMatrixFEM = YES in the data file.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// you can write the matrix (if stored)
Ah->mat_iterative_sym.WriteText("mat_iterative.dat");
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Computation/FemMatrixFreeClass.hxx
matCSR_iterative_sym, matCSR_iterative_unsym
The attribute matCSR_iterative_sym stores the finite element matrix if it is stored (and symmetric). If the matrix is unsymmetric, the attribute matCSR_iterative_unsym is used. To force the storage of the matrix, you can insert a line ExplicitMatrixFEM = YES in the data file. These matrices are constructed if the method CompressMatrix has been called previously.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// using CSR storage (to save memory)
Ah->CompressMatrix();
// you can write the matrix (if stored)
Ah->matCSR_iterative_sym.WriteText("mat_iterative.dat");
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Computation/FemMatrixFreeClass.hxx
var
This attribute stores a reference to the instance EllipticProblem.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> gt; Ah(var);
var.AddMatrixWithBC(Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah.MltVector(x, y); // y = A x
// var is present in the object Ah (here var and Ah.var refer to the same object)
Ah.var.SetPrintLevel(3);
Location :
Computation/FemMatrixFreeClass.hxx
Constructor of FemMatrixFreeClass
The only constructor takes an object EllipticProblem as argument. If you only have a base class of EllipticProblem (with a generic function that works for different equations), you can use the method GetNewIterativeMatrix.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> gt; Ah(var);
var.AddMatrixWithBC(Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah.MltVector(x, y); // y = A x
// if you are in a function with a base class of EllipticProblem :
FemMatrixFreeClass_Base<Real_wp>* Ah0 = var.GetNewIterativeMatrix(Real_wp(0));
var.AddMatrixWithBC(*Ah0, nat_mat);
delete Ah0;
Location :
Computation/FemMatrixFreeClass.hxx
SetCoefficientDirichlet
Syntax
| void SetCoefficientDirichlet(const Real_wp& coef) const |
This method changes the coefficient for the diagonal of Dirichlet dofs.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// computation of the finite element matrix
Matrix<Real_wp, General, ArrayRowSparse> A;
// we want void columns for Dirichlet => coef = 0
// default value is 1.0
var.SetCoefficientDirichlet(Real_wp(0));
var.AddMatrixWithBC(A, nat_mat);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
Harmonic/BoundaryConditionHarmonic.hxx Harmonic/BoundaryConditionHarmonicInline.cxx
SetCoefficientMatrix
Syntax
| void SetCoefficientMatrix(const GlobalGenericMatrix& coefs) const |
This method changes the mass, damping and stiffness coefficient for the iterative matrix. Usually it is not needed to call this method since AddMatrixWithBC already initializes these coefficients.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// if you want to change the coefficient afterwards (not recommended because boundary terms do not change)
nat_mat.SetCoefficientStiffness(2.0);
Ah.SetCoefficientMatrix(nat_mat);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
GetCoefMass
Syntax
| T GetCoefMass() const |
This method returns the mass coefficient for the iterative matrix.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// should return 2.0
Real_wp mass = Ah.GetCoefMass();
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
IsSymmetric
Syntax
| bool IsSymmetric() const |
This method returns true if the matrix is symmetric.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// symmetric matrix ?
bool sym = Ah.IsSymmetric();
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
FormulationDG
Syntax
| int FormulationDG() const |
This method returns the type of the formulation used. It can be equal to ElementReference_Base::CONTINUOUS, ElementReference_Base::DISCONTINUOUS or ElementReference_Base::HDG as explained in the description of dg_formulation.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// DG formulation ?
int dg_form = Ah.FormulationDG();
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
SetCondensedSolver
Syntax
| void SetCondensedSolver(CondensationBlockSolver_Fem*) |
This method sets the condensed solver used to assemble the matrix. This method should not be used in regular use (since it is already called when AddMatrixBC is called).
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
DirichletDofIgnored
Syntax
| bool DirichletDofIgnored() const |
This method returns true if Dirichlet dofs are ignored. If Dirichlet dofs are present (= not ignored), we set yi = 0 for rows associated with Dirichlet condition (where y = A x is the result of the matrix-vector product).
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// Dirichlet dofs treated ?
bool dirichlet = Ah.DirichletDofIgnored();
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
IgnoreDirichletDof
Syntax
| void IgnoreDirichletDof() |
This method forces Dirichlet dofs to be ignored. If Dirichlet dofs are present (= not ignored), we set yi = 0 for rows associated with Dirichlet condition (where y = A x is the result of the matrix-vector product.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// if you want to ignore Dirichlet dofs
// (default : Dirichlet dofs are treated)
Ah.IgnoreDirichletDof();
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
SetScaling
Syntax
| void SetScaling(VectReal_wp& scale_left, VectReal_wp& scale_right) |
This method sets the scaling factors to use if the matrix is not stored. This method is called when ScaleMatrix is used. ScaleMatrix handles both cases (matrix stored or not).
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// if you want to replace A by L A R (L and R are diagonal matrices)
// where L is the left scaling and R the right scaling :
VectReal_wp L(Ah.GetM()), R(Ah.GetM());
L.FillRand(); R.FillRand();
// best option : use ScaleMatrix (it will call SetScaling)
ScaleMatrix(Ah, L, R);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClassInline.cxx
SucceedInAffectingPointer
Syntax
| bool SucceedInAffectingPointer(Matrix*& ptr_A, Matrix*& ptr_Acsr) |
This method tries to initialize ptr_A (or ptr_Acsr if the matrix has been compressed) with the matrix stored in the object. If the method returns false, it means that no matrix has been found (pointers have not been initialized). In that case, the matrix is probably not stored, or the symmetry is not correct.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// for a symmetric matrix
Matrix<Real_wp, Symmetric, RowSymSparse>* A_csr;
Matrix<Real_wp, Symmetric, ArrayRowSymSparse>* A_stored;
bool success = Ah.SucceedInAffectingPointer(A_stored, A_csr);
// if success is false, it means that the matrix is either unsymmetric or not stored
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
InitSymmetricMatrix
Syntax
| void InitSymmetricMatrix() |
This method inits the object to a symmetric matrix. This method should not be called in regular use, since it is already called by AddMatrixWithBC.
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
InitUnsymmetricMatrix
Syntax
| void InitUnsymmetricMatrix() |
This method inits the object to an unsymmetric matrix. This method should not be called in regular use, since it is already called by AddMatrixWithBC.
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
ApplyRightScaling
Syntax
| void ApplyRightScaling(const Vector& B0, Vector& C0, Vector& B, Vector& C) |
This method applies the right scaling to vector B0 (B = R B0 where R is the right scaling) and inits C = C0. If no right scaling is required, B and C are initialized with B0 and C0. This method is used in the method MltAddFree to handle scaling of the matrix.
Example :
// if you specialize the class with your equation
class FemMatrixFreeClass<Real_wp, MyEquation> : public FemMatrixFreeClass_Eq<Real_wp, MyEquation>
{
public :
FemMatrixFreeClass(const EllipticProblem<MyEquation>& var_)
: FemMatrixFreeClass_Eq<Real_wp, MyEquation>(var_) {}
// product C0 = (L A R) B0
void MltAddFree(const GlobalGenericMatrix<Real_wp>& nat_mat,
const SeldonTranspose&, int level,
const VectReal_wp& B0, VectReal_wp& C0) const
{
VectReal_wp B, C;
// right scaling for B = R B 0
this->ApplyRightScaling(B0, C0, B, C);
// you do the matrix vector product without scaling C = A B
// ... (code to insert)
// finally left scaling for C0 = L C
this->ApplyLeftScaling(B0, C0, B, C);
}
};
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
ApplyLeftScaling
Syntax
| void ApplyLeftScaling(const Vector& B0, Vector& C0, Vector& B, Vector& C) |
This method applies the left scaling to vector C (C0 = L C where L is the left scaling). This method is used in the method MltAddFree to handle scaling of the matrix.
Example :
// if you specialize the class with your equation
class FemMatrixFreeClass<Real_wp, MyEquation> : public FemMatrixFreeClass_Eq<Real_wp, MyEquation>
{
public :
FemMatrixFreeClass(const EllipticProblem<MyEquation>& var_)
: FemMatrixFreeClass_Eq<Real_wp, MyEquation>(var_) {}
// product C0 = (L A R) B0
void MltAddFree(const GlobalGenericMatrix<Real_wp>& nat_mat,
const SeldonTranspose&, int level,
const VectReal_wp& B0, VectReal_wp& C0) const
{
VectReal_wp B, C;
// right scaling for B
this->ApplyRightScaling(B0, C0, B, C);
// you do the matrix vector product without scaling C = A B
// ... (code to insert)
// finally left scaling for C0 = L C
this->ApplyLeftScaling(B0, C0, B, C);
}
};
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
CompressMatrix
Syntax
| void CompressMatrix() |
This method compresses the matrices stored in the object. It consists of converting them into CSR storage (e.g. RowSparse instead of ArrayRowSparse) which requires less memory. The matrix vector product is also more efficient.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// for an iterative matrix (the matrix is not necessary stored, use FemMatrixFreeClass)
FemMatrixFreeClass_Base<Real_wp>* Ah = var.GetNewIterativeMatrix(Complex_wp(0));
var.AddMatrixWithBC(*Ah, nat_mat);
// with Ah, you can only compute matrix-vector products
VectReal_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand();
Ah->MltVector(x, y); // y = A x
// matrices are compressed (use of CSR storage)
Ah->CompressMatrix();
// do not forget to release the memory when Ah is no longer needed
delete Ah;
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
AddExtraBoundaryTerms
Syntax
| void AddExtraBoundaryTerms(const T& alpha, const Vector& B, Vector& C) |
This method adds the terms due to boundary conditions (or other models) contained in mat_boundary* to the vector C. It can be used to write a specialization of the class for your own equation.
Example :
// if you specialize the class with your equation
class FemMatrixFreeClass<Real_wp, MyEquation> : public FemMatrixFreeClass_Eq<Real_wp, MyEquation>
{
public :
FemMatrixFreeClass(const EllipticProblem<MyEquation>& var_)
: FemMatrixFreeClass_Eq<Real_wp, MyEquation>(var_) {}
// product C0 = (L A R) B0
void MltAddFree(const GlobalGenericMatrix<Real_wp>& nat_mat,
const SeldonTranspose&, int level,
const VectReal_wp& B0, VectReal_wp& C0) const
{
VectReal_wp B, C;
// right scaling for B
this->ApplyRightScaling(B0, C0, B, C);
// you do the matrix vector product without scaling C = A B
// ... (code to insert)
// contributions of boundary terms
this->AddExtraBoundaryTerms(Real_wp(1), B, C);
// finally left scaling for C0 = L C
this->ApplyLeftScaling(B0, C0, B, C);
}
};
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
SetNbDirichletCondition
Syntax
| void SetNbDirichletCondition(int n) |
This method sets the number of Dirichlet conditions, usually it corresponds to the number of right-hand-sides.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// for a single right hand side
Ah.SetNbDirichletCondition(1);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
ApplyDirichletCondition
Syntax
| void ApplyDirichletCondition(const SeldonTranspose& trans, Vector& b, int k=0) |
This method modifies the right hand side if hetereogenous Dirichlet condition is present. The new right hand side is equal to
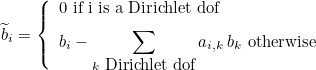
With this transformation, the hetereogeneous Dirichlet is converted into an homogeneous Dirichlet condition (with a symmetric finite element matrix). The values bk where k is a Dirichlet dof are stored in the object and used when ImposeDirichletCondition is called. If trans is equal to SeldonTranspose, we assume that the solution with the transpose of A is searched.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// for a single right hand side
Ah.SetNbDirichletCondition(1);
VectReal_wp rhs(Ah.GetM()); rhs.FillRand();
// we modify the right hand side to convert Dirichlet conditions to homogeneous ones
Ah.ApplyDirichletCondition(SeldonNoTrans, rhs);
// then you have to solve A x = rhs
// to do
VectReal_wp x(rhs.GetM()); x.Zero(); // etc
Cg(Ah, x, rhs, id_precond, iter); // solving with Cg for instance
// to get back to the solution (with hetereogeneous Dirichlet)
Ah.ImposeDirichletCondition(SeldonNoTrans, x);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
ImposeDirichletCondition
Syntax
| void ImposeDirichletCondition(const SeldonTranspose& trans, Vector& x, int k=0) |
This method sets the values of x with Dirichlet conditions given when ApplyDirichletCondition has been called.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// for two right hand sides
Ah.SetNbDirichletCondition(2);
VectReal_wp rhs(Ah.GetM()), rhs2(Ah.GetM()); rhs.FillRand(); rhs2.FillRand();
// we modify the right hand sides to convert Dirichlet conditions to homogeneous ones
Ah.ApplyDirichletCondition(SeldonNoTrans, rhs, 0);
Ah.ApplyDirichletCondition(SeldonNoTrans, rhs2, 1);
// then you have to solve A x = rhs
// to do
VectReal_wp x(rhs.GetM()), x2(rhs2.GetM()); x.Zero(); x2.Zero(); // etc
Cg(Ah, x, rhs, id_precond, iter); // solving with Cg for instance
Cg(Ah, x2, rhs2, id_precond, iter);
// to get back to the solution (with hetereogeneous Dirichlet)
Ah.ImposeDirichletCondition(SeldonNoTrans, x, 0);
Ah.ImposeDirichletCondition(SeldonNoTrans, x2, 1);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
SetDirichletCondition
Syntax
| void SetDirichletCondition(Matrix& A, int offset_row=0, int offset_col=0) |
This method modifies the matrix by removing rows (and/or columns) associated with Dirichlet dofs. For a symmetric matrix, the Dirichlet rows and columns are removed and replaced by a diagonal with a constant coefficient (usually one). This method does not need to be called, since it is already done in AddMatrixWithBC.
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
MltAddHetereogeneousDirichlet
Syntax
| void MltAddHetereogeneousDirichlet(const T& alpha, const SeldonTranspose& trans, const Vector& B, Vector& C) |
This method computes C = C + alpha A B with only columns a A associated with Dirichlet dofs.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
// product with only Dirichlet columns
VectReal_wp b(Ah.GetM()); b.FillRand();
VectReal_wp c(Ah.GetM()); c.Zero();
Ah.MltAddHetereogeneousDirichlet(Real_wp(1), SeldonNoTrans, b, c);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
InitDirichletCondition
Syntax
| void InitDirichletCondition(const Vector& b, int k=0) |
This method stores hetereogeneous Dirichlet condition contained in x. The values can then be retrieve by calling ImposeDirichletCondition.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
var.ComputeMeshAndFiniteElement(type_element); // mesh and finite element are constructed
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Real_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
nat_mat.SetCoefMass(2.0); // chaning the mass coefficient
// computation of the finite element matrix
FemMatrixFreeClass<Real_wp, ElasticEquation<Dimension3> > Ah;
var.AddMatrixWithBC(Ah, nat_mat);
VectReal_wp x(Ah.GetM()); x.FillRand();
// if you want to store values contained in x on Dirichlet dofs :
Ah.InitDirichletCondition(x);
// and retrieve them
VectReal_wp y(Ah.GetM()); y.Zero();
Ah.ImposeDirichletCondition(SeldonNoTrans, y);
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
MltAddFree
Syntax
| void MltAddFree(const GlobalGenericMatrix& nat_mat, const SeldonTranspose& trans, int level, const Vector& X, Vector& Y) |
This method adds to Y the matrix-vector product A X where A is the matrix associated with the current object. If trans is equal to SeldonTrans, we add AT X. MltAddFree is usually not called directly, but rather MltVector (or MltAddVector). These two functions will call MltAddFree in the case where the matrix is not stored. You can specialize MltAddFree to perform the matrix-vector product with your own equation (matrix-free implementation).
Example :
// if you specialize the class with your equation
class FemMatrixFreeClass<Real_wp, MyEquation> : public FemMatrixFreeClass_Eq<Real_wp, MyEquation>
{
public :
FemMatrixFreeClass(const EllipticProblem<MyEquation>& var_)
: FemMatrixFreeClass_Eq<Real_wp, MyEquation>(var_) {}
// product C0 = (L A R) B0
void MltAddFree(const GlobalGenericMatrix<Real_wp>& nat_mat,
const SeldonTranspose&, int level,
const VectReal_wp& B0, VectReal_wp& C0) const
{
VectReal_wp B, C;
// right scaling for B = R B 0
this->ApplyRightScaling(B0, C0, B, C);
// you do the matrix vector product without scaling C = A B
// ... (code to insert)
// finally left scaling for C0 = L C
this->ApplyLeftScaling(B0, C0, B, C);
}
};
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
GetExtrapolVariables
Syntax
| ExtrapolVariablesProductFEM<T, TypeEquation>& GetExtrapolVariables() |
This method returns the object storing additional variables needed to perform the matrix-vector product. You can also specialize the class ExtrapolVariablesProductFEM to store the variables needed to perform the matrix-vector product.
Example :
// if you specialize the class with your equation
class FemMatrixFreeClass<Real_wp, MyEquation> : public FemMatrixFreeClass_Eq<Real_wp, MyEquation>
{
public :
FemMatrixFreeClass(const EllipticProblem<MyEquation>& var_)
: FemMatrixFreeClass_Eq<Real_wp, MyEquation>(var_) {}
// product C0 = (L A R) B0
void MltAddFree(const GlobalGenericMatrix<Real_wp>& nat_mat,
const SeldonTranspose&, int level,
const VectReal_wp& B0, VectReal_wp& C0) const
{
VectReal_wp B, C;
// right scaling for B = R B 0
this->ApplyRightScaling(B0, C0, B, C);
// you do the matrix vector product without scaling C = A B
// ... (code to insert)
ExtrapolVariablesProductFEM<Real_wp, MyEquation>& var_extra = this->GetExtrapolVariables();
// finally left scaling for C0 = L C
this->ApplyLeftScaling(B0, C0, B, C);
}
};
Location :
Computation/FemMatrixFreeClass.hxx Computation/FemMatrixFreeClass.cxx
mesh
This attribute is the mesh used to complete the simultation. It is usually modified through data file (by inserting a line FileMesh = file_name).
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
// you can write the mesh on a file
var.mesh.Write("test.mesh");
Location :
Harmonic/VarGeometryProblem.hxx
Glob_PointsQuadrature
This attribute stores the quadrature points on all the elements. These points are computed when the method ComputeMassMatrix is called.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
// (second argument is false to keep quadrature points)
// (if the second argument is true, the quadrature points are cleared)
var.ComputeMassMatrix(true, false);
// you can display quadrature points of a given element
int num_elem = 5;
DISP(var.Glob_PointsQuadrature(num_elem));
// to retrieve one point :
int j = 7;
R2 single_pt = var.Glob_PointsQuadrature(num_elem)(j);
Location :
Harmonic/VarGeometryProblem.hxx
write_quadrature_points, write_quad_points_pml
If the attribute write_quadrature_points is true, the quadrature points are written in the file quadrature_points.dat when the method ComputeMassMatrix is called. If the attribute write_quad_points_pml is true, the quadrature points of PMLs are written, otherwise only quadrature points of elements in the physical domain are written. These attributes are usually modified by inserting a line WriteQuadraturePoints = YES NO_PML_POINTS in the data file.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// if you want to force quadrature points to be written
var.write_quadrature_points = true;
var.write_quad_points_pml = true; // with PMLs
// quadrature points and jacobian matrices are computed (and written if asked)
var.ComputeMassMatrix(true, false);
Location :
Harmonic/VarGeometryProblem.hxx
Glob_jacobian
This attribute stores the following quantities :
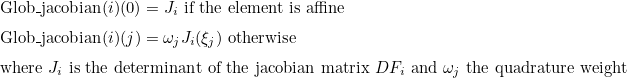
An element is affine if the transformation Fi is affine. In 2-D, it corresponds to straight triangles and parallelograms.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
int num_elem = 5;
bool affine = var.mesh.IsElementAffine(num_elem);
if (affine)
{
// affine elements, the jacobian is stored (without weight)
Real_wp jacob = var.Glob_jacobian(num_elem)(0);
}
else
{
// weighted jacobian on quadrature points
int j = 4;
Real_wp omJi = var.Glob_jacobian(num_elem)(j);
// if you want to recover the jacobian on the quadrature point => divide by the weight
const ElementReference<Dimension2, 1>& Fb = var.GetReferenceElementH1(num_elem);
Real_wp om = Fb.WeightsND(j); Real_wp jacob = omJi / om;
}
Location :
Harmonic/VarGeometryProblem.hxx
Glob_decomp_jacobian
This attribute stores the polynomial coefficients of the jacobian. They are computed only for elements that have a sparse mass matrix for straight elements. It can be checked by calling the method LinearSparseMassMatrix of the finite element.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
// polynomial coefficients of the jacobian
int num_elem = 11;
const ElementReference<Dimension2, 1>& Fb = var.GetReferenceElementH1(num_elem);
if (Fb.LinearSparseMassMatrix())
cout << "coefficients = " << var.Glob_decomp_jacobian(num_elem) << endl;
Location :
Harmonic/VarGeometryProblem.hxx
Glob_normale
This attribute stores the normales on quadrature points of faces (edges in 2-D) of the mesh. They are computed when the method ComputeMassMatrix is called.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
// normales for a given face
int num_face = 11; int num_pt = 2;
R2 normale = var.Glob_normale(num_face)(num_pt);
Location :
Harmonic/VarGeometryProblem.hxx
Glob_dsj
This attribute stores the surface integration elements on quadrature points of faces (edges in 2-D) of the mesh. They are computed when the method ComputeMassMatrix is called.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
// surface jacobian (used to compute surface integrals)
int num_face = 11; int num_pt = 2;
Real_wp ds = var.Glob_dsj(num_face)(num_pt);
Location :
Harmonic/VarGeometryProblem.hxx
OrthogonalElement
This attribute stores the type of orthogonality of the considered element. It is computed only for elements inside PML elements. In 2-D, it can take the following values:
- 0 : the element has diagonal jacobian matrices (the quadrilateral is a rectangle)
- 1 : at least one jacobian matrix is not diagonal
In 3-D, it can take the following values:
- 0 : the element has diagonal jacobian matrices (the hexahedron is a rectangular parallelepiped)
- 1 : the element has jacobian matrices with zeros on last row and last column (except the diagonal coefficient). It corresponds to hexahedra that are obtained by extrusion in z-direction.
- 2 : other elements
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
// orthogonal element ?
int num_elem = 13;
int ortho = var.OrthogonalElement(num_elem);
Location :
Harmonic/VarGeometryProblem.hxx
Glob_DFjm1
This attribute stores the following quantities :
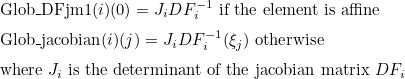
An element is affine if the transformation Fi is affine. In 2-D, it corresponds to straight triangles and parallelograms.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
int num_elem = 5;
bool affine = var.mesh.IsElementAffine(num_elem);
if (affine)
{
// affine elements, only one matrix is stored
Matrix2_2 jacob_dfjm1 = var.Glob_DFjm1(num_elem)(0);
}
else
{
// matrices J_i DF_i^{-1} on quadrature points
int j = 4;
Matrix2_2 jacob_dfm1 = var.Glob_DFjm1(num_elem)(j);
}
Location :
Harmonic/VarGeometryProblem.hxx
IsNewFace
This attribute is used to know if the normale is outgoing to the element. If IsNewFace(i)(j) is true, the normales stored in Glob_normale are outgoing to the element i.
Example :
EllipticProblem<LaplaceEquation<Dimension2> > var;
var.InitIndices(100);
var.SetTypeEquation("LAPLACE");
ReadInputFile(input_file, var); // parameters of the ini file are read
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
int num_elem = 5;
int num_loc = 2; // local boundary of element
bool new_face = var.IsNewFace(num_elem)(num_loc);
int num_face = var.mesh.Element(num_elem).numBoundary(num_loc);
int num_pt = 1;
R2 normale = var.Glob_normale(num_face)(num_pt);
// changing sign of normale to enforce an outgoing normale to element num_elem
if (!new_face)
normale = -normale;
Location :
Harmonic/VarGeometryProblem.hxx
GetReferenceInfinity
Syntax
| int GetReferenceInfinity() const |
This method returns the reference associated with the medium at infinity. This reference is used for absorbing boundary conditions (in order to know physical indexes at infinity). By default, it is set to -1 (indexes are equal to one at infinity in this case). This value is modified by inserting a line ReferenceInfinity = 1 in the data file.
Example :
EllipticProblem<ElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// reference for infinity ?
int ref = var.GetReferenceInfinity();
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetWaveVector, SetWaveVector
Syntax
| R_N GetWaveVector() const |
| void SetWaveVector(const R_N& u) const |
The method GetWaveVector returns the wave vector k. It is used to define the plane wave:
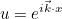
The wave vector can be modified by calling SetWaveVector or by inserting lines with Frequency and IncidentAngle.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// wave vector ?
R3 k = var.GetWaveVector();
Real_wp omega = var.GetOmega();
// if you modify the norm of k, it is better to call SetOmega to change the frequency
// SetOmega updates the wave vector such that omega = || k ||
var.SetOmega(2.0*omega);
k = -2.0*k;
var.SetWaveVector(k);
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetPolarization
Syntax
| VectReal_wp GetPolarization() const |
| void GetPolarization(Vector& polar) const |
The method GetPolarization returns the polarization vector E0. It is used to define the plane wave (for vectorial equations):
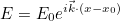
The polarization can be modified by calling SetPolarization or by inserting lines with Polarization. The polarization vector is also used in other sources (volume sources or Dirac) if the user did not provide a specific direction.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// polarization
VectReal_wp polar = var.GetPolarization();
//if you need a tiny vector
R3 E0; var.GetPolarization(E0);
// or a complex vector
VectComplex_wp Pc;
var.GetPolarization(Pc);
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetPolarizationGrad
Syntax
| VectReal_wp GetPolarizationGrad() const |
| void GetPolarizationGrad(Vector& polar) const |
The method GetPolarizationGrad returns the polarization vector E0. It is used in the case of a gradient of Dirac source :
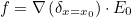
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetPhaseOrigin
Syntax
| R_N GetPhaseOrigin() const |
This method returns the origin x0 of plane waves such that the phase is 0 at the origin. It is used to define the plane wave :
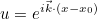
The origin can be modified by inserting lines with OriginePhase. The origin is also used for the Dirac source if the user did not provide a specific origin.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// origin for plane waves
R3 x0 = var.GetPhaseOrigin();
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
SetPolarization
Syntax
| void SetPolarization(TinyVector P) const |
This method sets the polarization (used for plane waves as explained in GetPolarization. Another solution is to insert a line Polarization = 0.0 0.0 1.0 in the data file.
Example :
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to set manually the polarization
R3 P(0.2, 0.5, 0.8);
var.SetPolarization(P);
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
FinalizeComputationVaryingIndices
Syntax
| void FinalizeComputationVaryingIndices() |
This virtual method is automatically called when ComputeMassMatrix is called such that the user can treat the physical indexes that have been computed. In regular use, this method does not need to be called.
Example :
// if you derive your own EllipticProblem:
template<>
class EllipticProblem<MyEquation> : public VarHarmonic<MyEquation>
{
public:
// overloading the method
void FinalizeComputationVaryingIndices() { // your own treatment }
};
int main()
{
EllipticProblem<MyEquation> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix(); // the method FinalizeComputationVaryingIndices() is called here
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
AllocateMassMatrices
Syntax
| void AllocateMassMatrices() |
This virtual method is automatically called when ComputeMassMatrix is called such that the user can allocate arrays to store datas needed to the computation of elementary matrices. In regular use, this method does not need to be called.
Example :
class MyEquation
{
public:
template<class TypeEquation>
void ComputeMassMatrix(EllipticProblem<TypeEquation>& var, int i, const ElementReference_Dim<Dimension3>& Fb)
{ // computation of some variables }
};
// if you derive your own EllipticProblem:
template<>
class EllipticProblem<MyEquation> : public VarHarmonic<MyEquation>
{
public:
// overloading the method
void AllocateMassMatrices() { // allocation of arrays that will be used in ComputeMassMatrix of MyEquation (method above) }
};
int main()
{
EllipticProblem<MyEquation> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix(); // the method AllocateMassMatrices() is called here
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
DoNotComputeGrid
Syntax
| void DoNotComputeGrid() |
This method can be used if you do not want to compute interpolation grids when ComputeMeshAndFiniteElement is called.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to compute the interpolation grid only when the solution is interpolated
var.DoNotComputeGrid();
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("QUADRANGLE_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetLocalUnknownVector
Syntax
| void GetLocalUnknownVector(const Vector& u, int i, Vector u_loc) |
This method can be used to retrieve the local components of the vector u in the element i as explained in GetLocalUnknownVector.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// creation of the linear solver
All_LinearSolver* solver = var.GetNewLinearSolver();
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// to compute the right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b
VectComplex_wp x = b; solver->ComputeSolution(x);
// when you no longer need the solver, you can release the memory
delete solver;
// if you want to retrieve the solution on a given element
int num_elem = 23;
TinyVector<VectComplex_wp, 3> x_loc; // here 3 components for elatic equation
var.GetLocalUnknownVector(x, num_elem, x_loc);
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
AddLocalUnknownVector
Syntax
| void AddLocalUnknownVector(T alpha, const Vector& u_loc, int i, Vector u) |
This method can be used to add local contributions (of the element i) to the global vector u as explained in AddLocalUnknownVector.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
ModifyLocalComponentVector
Syntax
| void ModifyLocalComponentVector(Vector& u_loc, int i) |
This method can be used to modify the local components of the vector u_loc in the element i as explained in ModifyLocalComponentVector. The method GetLocalUnknownVector consists of extracting the local values of a global vector and then calling this function.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// creation of the linear solver
All_LinearSolver* solver = var.GetNewLinearSolver();
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// to compute the right hand side
VectComplex_wp b(var.GetNbDof());
var.ComputeRightHandSide(b);
// and solve the linear system A x = b
VectComplex_wp x = b; solver->ComputeSolution(x);
// when you no longer need the solver, you can release the memory
delete solver;
// if you want to retrieve the solution on a given element
int num_elem = 23;
Vector<VectComplex_wp, 3> x_loc(3);
// you can extract manually the values
int nb_dof = var.GetReferenceElement(num_elem).GetNbDof();
x_loc(0).Reallocate(nb_dof); x_loc(1).Reallocate(nb_dof);
x_loc(2).Reallocate(nb_dof);
for (int j = 0; j < nb_dof; j++)
{
int num_dof = var.GetMeshNumbering(0).Element(num_elem).GetNumberDof(j);
x_loc(0)(j) = x(num_dof);
x_loc(1)(j) = x(var.offset_dof_unknown(0) + num_dof);
x_loc(2)(j) = x(var.offset_dof_unknown(1) + num_dof);
}
// then we modify the values to take into account signs of dofs (or linear operators if present)
var.ModifyLocalComponentVector(x_loc, num_elem);
// in this example, it is better to call directly GetLocalUnknownVector
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
ModifyLocalUnknownVector
Syntax
| void ModifyLocalUnknownVector(Vector& u_loc, int i) |
This method can be used to modify the local components of the vector u_loc in the element i as explained in ModifyLocalUnknownVector. The method AddLocalUnknownVector consists of calling this function and of adding the local values to a global vector. This function is the transpose operation of the function ModifyLocalComponentVector.
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetGlobalUnknownVector
Syntax
| void GetGlobalUnknownVector(Vector& u_loc, int i) |
This method can be used to modify the local components of the vector u_loc in the element i as explained in GetGlobalUnknownVector. The vector can then be copied directly on a global vector as shown in the example below
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points and jacobian matrices are computed
var.ComputeMassMatrix();
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the projection of a function on degrees of freedom manually,
// you can compute contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval;
Vector<VectComplex_wp> contrib(1);
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemDof(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsDof());
contrib(0).Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsDof(); j++)
feval(j) = exp(-Norm2(pts.GetPointDof(i)));
Fb.ComputeProjectionDofRef(feval, contrib(0));
var.GetGlobalUnknownVector(contrib(0), i); // taking into account signs or linear operators
// then copying the values in the global vector
for (int j = 0; j < Fb.GetNbDof(); j++)
{
int num_dof = var.GetMeshNumbering(0).Element(num_elem).GetNumberDof(j);
b(num_dof) = contrib(0)(j);
}
}
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetNbComponentsType
Syntax
| int GetNbComponentsType(int type) |
This method returns the number of components for the unknown for a given finite element. If type is equal to 1 (for H1 elements), it returns 1. If type is equal to 2 or 3(for edge and facet elements) it returns the dimension.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// number of components for edge elements ?
int nb_comp_u = var.GetNbComponentsType(2);
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetNbComponentsGradType
Syntax
| int GetNbComponentsGradType(int type) |
This method returns the number of components for the derivatives of an unknown for a given finite element. If type is equal to 1 (for H1 elements), it returns the dimension (number of components of the gradient). If type is equal to 2 (for edge elements) it returns the number of components of the curl. If type is equal to 3 (for edge elements), it returns one (number of components of the divergence.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// number of components for the curl of edge elements ?
int nb_comp_curl = var.GetNbComponentsGradType(2);
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetNbComponentsAll
Syntax
| int GetNbComponentsAll(int nb_u = 0) |
This method returns the number of components for all the unknowns. The second argument if optional and means that we consider only the first nb_u unknowns.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// cumulative number of components for all the unknowns
int nb_comp_all = var.GetNbComponentsAll();
}
Location :
Harmonic/VarGeometryProblem.hxx Harmonic/VarGeometryProblem.cxx
GetNbComponentsGradientAll
Syntax
| int GetNbComponentsGradientAll(int nb_u = 0) |
This method returns the number of components for the derivatives of all the unknowns. The second argument if optional and means that we consider only the first nb_u unknowns.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// cumulative number of components for the gradient of all the unknowns
int nb_grad_all = var.GetNbComponentsGradientAll();
}
Location :
Harmonic/VarGeometryProblem.h_xx Harmonic/VarGeometryProblem.cxx
GetNbComponentsHessianAll
Syntax
| int GetNbComponentsHessianAll(int nb_u = 0) |
This method returns the number of components for the hessians of all the unknowns. The second argument if optional and means that we consider only the first nb_u unknowns.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// cumulative number of components for the hessian matrices of all the unknowns
int nb_hess_all = var.GetNbComponentsHessianAll();
}
Location :
Harmonic/VarGeometryProblem.h_xx Harmonic/VarGeometryProblem.cxx
GetMeshNumbering
Syntax
| const MeshNumbering<Dimension>& GetMeshNumbering(int n = 0) const |
This method gives access to the n-th mesh numbering.
Example :
EllipticProblem<LaplaceEquationDG<Dimension2> > var;;
// constructing the problem (mesh, finite element)
All_LinearSolver* solver;
var.ConstructAll("test.ini", "QUADRANGLE_LOBATTO", "LAPLACE_DG", solver);
// if you want to retrieve the mesh numbering for the main unknown
const MeshNumbering<Dimension2>& mesh_num = var.GetMeshNumbering();
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblemInline.cxx
WriteNodalPointsMesh
Syntax
| void WriteNodalPointsMesh() |
This method writes the nodal points of the mesh in the file nodal_points.dat. This file can be read by using the function ReadNodalPoints (in the package visuND of Python). It is also used by the files src/Program/Test/write_index*.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// you can write nodal points of the mesh
var.WriteNodalPointsMesh();
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblemInline.cxx
LocalizePointsBoundaryElement
Syntax
| void LocalizePointsBoundaryElement( | const VectR_N& Points, int num_elem, int num_loc, FjInverseProblem& inverseFj, |
| VectR_N& local_pts, IVect& num_pts) |
This method computes the local positions of points given as argument in the element. Only points located on the boundary will contribute to the array local_pts. We have the relation Points(num_pts(k)) = Fi(local_pts(k)). From the array Points, the method fills the arrays local_pts and num_pts.
Parameters
- Points (in)
- points to localize on the boundary of the element
- mat_elem(in)
- element number
- num_loc (in)
- local position of the boundary
- inverseFj (out)
- object used to invert transformation Fi
- local_pts (out)
- local coordinates of points located on the boundary
- num_pts (in)
- numbers of the points localized on the boundary
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// we want to localize some points on a face of the mesh
int num_elem = 11, num_loc = 2; // face is the local face 2 of element 11
VectR3 Points(4);
Points(0).Init(2.0, 0.8, 1.2); // etc
FjInverseProblem<Dimension3> fj_inv;
VectR3 local_pts; IVect num_pts;
var.LocalizePointsBoundaryElement(Points, num_elem, num_loc, fj_inv, local_pts, num_pts);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
UseNumericalIntegration
Syntax
| bool UseNumericalIntegration( | int num_elem) |
This method returns true if an integral over the element num_elem needs a numerical integration. It is the case if the physical indexes are varying inside the element or if the transformation Fi is not affine.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_elem = 17;
bool varying = var.UseNumericalIntegration(num_elem); // integrals will be computed numerically ?
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
FaceHasToBeConsideredForBoundaryIntegral
Syntax
| bool FaceHasToBeConsideredForBoundaryIntegral( | int num_face) |
This method returns true if an integral over the face num_face (edge in 2-D) will be needed to compute the finite element matrix. It is the case for discontinuous Galerkin formulations, or for faces located on periodic boundaries (weak formulation of periodic conditions).
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_face = 17;
bool int_face = var.FaceHasToBeConsideredForBoundaryIntegral(num_face); // integrals over face num_face are needed ?
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetWeightedJacobian
Syntax
| Real_wp GetWeightedJacobian( | int num_elem, int j, bool affine, ElementGeomReference& elt) |
This method returns the determinant of the jacobian matrix DFi multiplied by the quadrature weight, such that it can be used to evaluate a volume integral.
Parameters
- num_elem(in)
- element number
- j (in)
- local number of the quadrature point
- affine (in)
- true if the transformation Fi is affine
- elt (in)
- object containing shape functions
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_elem = 21; int j = 7;
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(num_elem);
bool affine = var.mesh.IsElementAffine(num_elem);
// jacobian Ji multiplied by omega_k (weight) :
Real_wp omJi = var.GetWeightedJacobian(num_elem, j, affine, Fb.GetGeometricElement());
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetSurfaceWeightedJacobian
Syntax
| Real_wp GetWeightedJacobian( | int num_elem, int num_loc, int num_face, int j, ElementGeomReference& elt) |
This method returns the surface element integration dsi multiplied by the quadrature weight, such that it can be used to evaluate a surface integral.
Parameters
- num_elem(in)
- element number
- num_loc(in)
- local number of the face
- num_face(in)
- global number of the face
- j (in)
- local number of the quadrature point
- elt (in)
- object containing shape functions
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_elem = 21, num_loc = 1; int j = 7;
int num_face = var.mesh.Element(num_elem).numBoundary(num_loc);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(num_elem);
// surfacic jacobian Ji multiplied by omega_k (weight) :
Real_wp omDsi = var.GetSurfaceWeightedJacobian(num_elem, num_loc, num_face, j, Fb.GetGeometricElement());
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetInverseJacobianMatrix
Syntax
| Real_wp GetInverseJacobianMatrix( | int num_elem, int j, bool affine, ElementGeomReference& elt, |
| MatrixN_N& dfjm1, Real_wp& jacob, Real_wp& jacob_weighted) |
This method can be used to retrieve the inverse of the jacobian matrix (i.e. DFi-1). It retrieves also the determinant of the jacobian matrix DFi multiplied by the quadrature weight, such that it can be used to evaluate a volume integral.
Parameters
- num_elem(in)
- element number
- j (in)
- local number of the quadrature point
- affine (in)
- true if the transformation Fi is affine
- elt (in)
- object containing shape functions
- dfjm1 (out)
- inverse of jacobian matrix
- jacob (out)
- Ji = det(DFi)
- jacob_weighted (out)
- Ji multiplied by the quadrature weight
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_elem = 21; int j = 7;
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(num_elem);
bool affine = var.mesh.IsElementAffine(num_elem);
// jacobian Ji multiplied by omega_k (weight), and inverse of jacobian matrix
Matrix3_3 inv_dfj; Real_wp jacob, omJi;
var.GetInverseJacobianMatrix(num_elem, j, affine, Fb.GetGeometricElement(),
inv_dfj, jacob, omJi);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
FillQuadratureJacobian
Syntax
| void FillQuadratureJacobian( | int num_elem, int N, ElementGeomReference& elt, |
| const VectR_N& s, SetPoints& pts_elem, SetMatrices& mat_elem) |
This method can be used to fill pts_elem with quadrature points and mat_elem with jacobian matrices DFi on quadrature points.
Parameters
- num_elem(in)
- element number
- N (in)
- number of quadrature points
- elt (in)
- object containing shape functions
- s (in)
- vertices of the element
- pts_elem (inout)
- object containing image of points by transformation Fi
- mat_elem (out)
- object containing jacobian matrices
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
int num_elem = 21;
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(num_elem);
int N = Fb.GetNbPointsQuadratureInside();
VectR3 s; var.mesh.GetVerticesElement(num_elem, s);
SetPoints<Dimension3> PointsElem; SetMatrices<Dimension3> MatricesElem;
// if we want to fill PointsElem and MatricesElem (on quadrature points only)
var.FillQuadratureJacobian(num_elem, N, Fb.GetGeometricElement(),
s, PointsElem, MatricesElem);
// then you can use them
DISP(MatricesElem.GetPointQuadrature(2));
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
ComputeLocalMassMatrix
Syntax
| void ComputeLocalMassMatrix( | int num_elem, int N, bool linear_sparse_mass, |
| SetPoints& pts_elem, SetMatrices& mat_elem, IVect&OrderFace, ElementGeomReference& elt) |
This method is automatically called by ComputeMassMatrix by each element. This method is virtual such that the user can add specific computations for his own equation. In regular use, this method should not be called.
Parameters
- num_elem(in)
- element number
- N (in)
- number of quadrature points
- linear_sparse_mass (in)
- true if the mass matrix for affine elements if sparse
- pts_elem (inout)
- object containing image of points by transformation Fi
- mat_elem (inout)
- object containing jacobian matrices
- OrderFace (inout)
- order of quadrature for each face
- elt (in)
- object containing shape functions
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
ComputeMassMatrix
Syntax
| void ComputeMassMatrix( | bool compute_rho = true, bool delete_points=true) |
This method computes geometric quantities such as jacobian matrices and determinants, outgoing normales. If compute_rho is true (default value), the physical indexes (such as rho, mu and sigma for Helmholtz equation) are evaluated at quadrature points (for varying indexes). If delete_points is false, the quadrature points will be stored in Glob_PointsQuadrature. Before computing the finite element matrix, the method ComputeMassMatrix needs to be called. The name of the method "ComputeMassMatrix" may be misleading since the actual mass matrix is not computed, but rather quantities needed to compute the mass matrix.
Parameters
- compute_rho(optional)
- if true, physical indexes are evaluated at quadrature points
- delete_points (optional)
- if true, the computed quadrature points are not stored
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
ClearMassMatrix
Syntax
| void ClearMassMatrix() |
This method clears the geometric quantities that have been computed in the method ComputeMassMatrix. It can be useful to release memory.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// creation of the linear solver
All_LinearSolver* solver = var.GetNewLinearSolver();
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// if you selected a direct solver, no need to store geometric stuff
var.ClearMassMatrix();
// and solve the linear system A x = b
VectComplex_wp b(var.GetNbDof()), x; b.FillRand();
x = b; solver->ComputeSolution(x);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
ComputeVariableOrder
Syntax
| void ComputeVariableOrder() |
This method affects orders for each element in the case where the user selects a variable order by inserting for instance a line :
OrderDiscretization = MEAN_EDGE AUTO 0.5
in the data file. More details are given in the description of OrderDiscretization. The method ComputeVariableOrder is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetPhysicalCoefficientMesh
Syntax
| Mesh<Dimension>& GetPhysicalCoefficientMesh( | int i, string file_name, int r, bool same_mesh, |
| VectString& all_names, Vector<Mesh>& all_mesh) |
This method returns the i-th mesh associated with the name file_name and with the order r. If the mesh already exists in the array all_mesh (with indices between 0 and i-1), the mesh is returned. If the mesh does not exist, the mesh is read from the file file_name and returned. If the mesh is created, all_names(i) contains the file name and all_mesh(i) the created mesh. This method is used for varying indexes based on meshes in order to read a mesh only once (to avoid multiple creations of a same mesh). In regular use, this method does not need to be called.
Parameters
- i (in)
- mesh number
- file_name (in)
- name of the file where the mesh is stored
- r (in)
- order of approximation
- same_mesh (in)
- if true the i-th mesh is actually the same as the current mesh
- all_names (inout)
- names of the created meshes
- all_mesh (inout)
- created meshes
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetPhysicalCoefInterp
Syntax
| Vector<FiniteElementInterpolator>& GetPhysicalCoefInterp( | int r, const Mesh<Dimension> meshb, TinyVector<IVect, 4>& order_mesh, |
| Vector<Vector<FiniteElementInterpolator>>& all_interp, IVect& order_interp) |
This method computes the projector from nodal points of meshb to quadrature points of the finite elements stored in the current object. If the projector is already computed (and present in all_interp), the method returns the projector. If the projector is not present, it is created (and added to the array all_interp) and returned. In regular use, this method does not need to be called. This method is used to evaluate the varying indexes on quadrature points.
Parameters
- r (in)
- order of approximation associated with meshb
- meshb (in)
- mesh of order r
- order_mesh (in)
- orders present in the current object (instance of VarGeometryProblem)
- all_interp (in)
- list of interpolators previously computed that will be updated
- order_interp (inout)
- list of orders for all_interp
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetPhysicalCoefInterpSurf
Syntax
| Vector<FiniteElementInterpolator>& GetPhysicalCoefInterp( | int r, const Mesh<Dimension> meshb, TinyVector<IVect, 4>& order_mesh, |
| Vector<Vector<FiniteElementInterpolator>>& all_interp, IVect& order_interp) |
This method computes the projector from surfacic nodal points of meshb to surfacic quadrature points of the finite elements stored in the current object. If the projector is already computed (and present in all_interp), the method returns the projector. If the projector is not present, it is created (and added to the array all_interp) and returned. In regular use, this method does not need to be called. This method is used to evaluate the varying indexes on quadrature points of the faces.
Parameters
- r (in)
- order of approximation associated with meshb
- meshb (in)
- mesh of order r
- order_mesh (in)
- orders present in the current object (instance of VarGeometryProblem)
- all_interp (in)
- list of interpolators previously computed that will be updated
- order_interp (inout)
- list of orders for all_interp
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
CheckInputMesh
Syntax
| void CheckInputMesh() |
This method checks the mesh and stops the program if the mesh is not correct. This method is virtual, such that it can be overloaded in derived classes in order to add some specific verifications. The method CheckInputMesh is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
GetVaryingIndices
Syntax
| void GetVaryingIndices( | Vector<PhysicalVaryingMedia<Complex_wp>*>& rho_cplx, Vector<PhysicalVaryingMedia<Real_wp>*>& rho_real |
| IVect& num_ref, IVect& num_index, IVect& num_component, | |
| VectBool& compute_grad, VectBool& compute_hess) |
This method retrieves all the variable physical indexes. It is virtual such that it differs for each equation. If you define your own set of equations, you need to overload this method and fill the varying indexes given as argument. If there are no varying indexes, the method should be empty. The method GetVaryingIndices is automatically called by ComputeMassMatrix, it should not be called in a regular use.
Parameters
- rho_cplx (out)
- list of complex varying indexes
- rho_real (out)
- list of real varying indexes
- num_ref (out)
- reference associated with each varying index
- num_index (out)
- number associated with each varying index
- num_component (out)
- component number associated with each varying index
- compute_grad (out)
- if compute_grad(i) is true, it means that the gradient of varying index i is needed
- compute_hess (out)
- if compute_hess(i) is true, it means that the hessian of varying index i is needed
Example :
// if you derive your own EllipticProblem:
template<>
class EllipticProblem<MyEquation> : public VarHarmonic<MyEquation>
{
public:
// overloading the method GetVaryingIndices
void GetVaryingIndices(Vector<PhysicalVaryingMedia<Dimension, Complex_wp<* >& rho_complex,
Vector<PhysicalVaryingMedia<Dimension, Real_wp>* >& rho_real, IVect& num_ref,
IVect& num_index, IVect& num_component, Vector<bool>& compute_grad,
Vector<bool>& compute_hess)
{
// no varying index => method is left empty
}
};
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
ComputeStoreCoefficientsPML
Syntax
| void ComputeStoreCoefficientsPML( | int num_elt_pml, int num_elem, const VectR_N& AllPoints) |
This method computes and stores damping coefficients in PMLs. It is a virtual method such that you can overlad it in a derived class. The method ComputeStoreCoefficientsPML is automatically called by ComputeMassMatrix, it should not be called in a regular use.
Parameters
- num_elt_pml (in)
- local element number (in PMLs)
- num_elem (in)
- element number
- AllPoints (in)
- quadrature points of the considered element
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarGeometryProblem.cxx
PointsQuadInsideND
Syntax
| VectR_N PointsQuadInsideND(int i) |
This method returns the quadrature points inside the reference element (for instance the unit cube if the element i is an hexahedron). The reference element is associated with the real element i.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points inside the reference element
int num_elem = 12;
VectR3 pts_quad_ref = var.PointsQuadInsideND(num_elem);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblemInline.cxx
PointsQuadratureBoundary
Syntax
| const VectR_Nm1& PointsQuadratureBoundary(int i, int num_loc) |
This method returns the quadrature points on the surface reference element (for instance the unit square if the face num_loc of the element i is a quadrilateral). The reference element is associated with the real element i.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// quadrature points for the unit square (or unit triangle)
int num_elem = 12, num_loc = 2;
VectR2 pts_quad_surf = var.PointsQuadratureBoundary(num_elem, num_loc);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblemInline.cxx
PointsDofBoundary
Syntax
| const VectR_Nm1& PointsDofBoundary(int i, int num_loc) |
This method returns the dof points on the surface reference element (for instance the unit square if the face num_loc of the element i is a quadrilateral). The reference element is associated with the real element i.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// dof points for the unit square (or unit triangle)
int num_elem = 12, num_loc = 2;
VectR2 pts_dof_surf = var.PointsDofBoundary(num_elem, num_loc);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblemInline.cxx
GetShapeElement
Syntax
| const ElementGeomReference& GetShapeElement(int i) |
This method returns the geometric reference element (that handles only shape functions). The reference element is associated with the real element i.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
// if you only need to manipulate shape functions (for geometry)
int num_elem = 14;
const ElementGeomReference<Dimension3>& Fb = var.GetShapeElement(num_elem);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblemInline.cxx
ConstructFiniteElement
Syntax
| void ConstructFiniteElement(string name_elt) |
This method constructs the finite elements needed (depending on the required orders of approximation). This method is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
ClearFiniteElement
Syntax
| void ClearFiniteElement() |
This method clears the finite elements stored in the class.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
UpdateInterpolationElement
Syntax
| void UpdateInterpolationElement() |
This method updates the finite elements (without reconstructing them) in the case where the orders of approximation are changed.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
SplitMeshForParallelComputation
Syntax
| void SplitMeshForParallelComputation(string name_elt) |
This method splits the mesh into several parts (depending on the number of MPI nodes) and distributes it between the processors. This method is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/DistributedProblem.cxx
SplitSubdomains
Syntax
| void SplitSubdomains(string name_elt) |
This method splits the mesh into several parts (depending on the number of MPI nodes) and distributes it between the processors. This method is an intermediary function called by SplitMeshForParallelComputation, it should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/DistributedProblem.cxx
ComputeNumberOfDofs
Syntax
| void ComputeNumberOfDofs() |
This method computes the total number of degrees of freedom. This method is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use. This method is virtual such that it can be overloaded if you need to have additional degrees of freedom.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
PutOtherGlobalDofs
Syntax
| void PutOtherGlobalDofs() |
This method is called only in parallel. It updates arrays such as MatchingDofOrig_Subdomain to have consistent dofs in parallel. This method is automatically called by ComputeMeshAndFiniteElement, it should not be called in a regular use. This method is virtual such that it can be overloaded if you need to add a special treatment.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
CheckContinuity
Syntax
| void CheckContinuity() |
This method checks that the basis functions achieve the claimed continuity. For H1 discretized with scalar finite elements, the basis functions should be continuous. For H(curl) discretized with edge elements, the tangential trace of basis functions should be continuous. For H(div) discretized with facet elements, the normal trace of basis functions should be continuous. This method is expensive and was mainly used for debugging the finite element classes. It is automatically called by ComputeMeshAndFiniteElement for a print level greater or equal to 12.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
PartMeshTransmission
Syntax
| void PartMeshTransmission() |
This method is meaningful when transmission conditions are present in the considered problem, for instance :

When continuous finite elements are used, degrees of freedom located on the interface need to be duplicated, such that the solution is discontinuous across the interface. This feature is achieved by modifying the mesh, the vertices on the interface are duplicated, the method PartMeshTransmission performs this operation on this mesh. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
TreatTransmission
Syntax
| void TreatTransmission(const IVect& epart ) |
This method is meaningful when transmission conditions are present in the considered problem. This method mainly computes the corresponding degrees of freedom located at the interface. It also computes stuff for parallel execution, that is why the array epart (containing the processor number for each element) is required. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
SendTransmissionDofs
Syntax
| void SendTransmissionDofs(const IVect& epart , int& nb_surface, int& nb_ddl , IVect& InfoSurf , IVect& InfoMatch ) |
This method is meaningful when transmission conditions are present in the considered problem. This method mainly send the number of degrees of freedom (located at the interface) to other processors. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
DistributeTransmissionDofs
Syntax
| void DistributeTransmissionDofs(int& nb_surface, int& nb_ddl , IVect& InfoSurf , IVect& InfoMatch ) |
This method is meaningful when transmission conditions are present in the considered problem. This method mainly distributes degrees of freedom (located at the interface) among the processors. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
TreatGibc
Syntax
| void TreatGibc(const IVect& epart) |
This method is meaningful when generalized impedance boundary conditions (GIBC) are present in the considered problem. This method mainly finds the dof numbers of degrees of freedom located on the surface when the GIBC are set. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
InitGibcReferences
Syntax
| void InitGibcReferences(int N) |
This method is meaningful when generalized impedance boundary conditions (GIBC) are present in the considered problem. This method provides to the class managing GIBC the number of references present in the mesh. This method is automatically called by ComputeMeshAndFiniteElement as soon as transmission conditions are present. This method should not be called in a regular use.
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblem.cxx
ComputeEnHnOnBoundary
Syntax
| void ComputeEnHnOnBoundary(const MeshInterpolationFEM& interp, const Vector& u, Vector& trace_en, Vector& trace_hn, bool assemble=true, bool compute_hn = true) |
This method computes the trace of the solution (E x n for Maxwell's equations) on a surface. If compute_hn is true, it computes also the trace of the derivative (H x n for Maxwell's equations).
Parameters
- interp (in)
- object storing informations about the surface where the trace is computed
- u (in)
- solution to interpolate
- trace_en (out)
- trace of the solution (E x n)
- trace_hn (out)
- trace of the derivative of the solution
- assemble (optional)
- if true, the values of other processors are gathered
- compute_hn (optional)
- if true, the trace of the derivative is computed
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
GlobalGenericMatrix<Complex_wp> nat_mat; // this object is used to store mass, damping and stiffness coefficients
// creation of the linear solver
All_LinearSolver* solver = var.GetNewLinearSolver();
// to factorize the matrix (or prepare the computation if an iterative solver is selected)
solver->PerformFactorizationStep(nat_mat);
// and solve the linear system A x = b
VectComplex_wp b(var.GetNbDof()), x; b.FillRand();
x = b; solver->ComputeSolution(x);
MeshInterpolationFEM<Dimension3> interp;
interp.SetGaussQuadrature(4); // defining quadrature points
interp.InitProjectionSurface(var.mesh); // computing the interpolation operators
// references defining the surface (ref_cond(i) = 1)
IVect ref_cond(var.mesh.GetNbReferences()+1); ref_cond.Zero();
ref_cond(3) = 1; ref_cond(5) = 1; // here surfaces of reference 3 and 5 are considered
// computing the surface mesh (with normales, jacobian matrices, etc)
Mesh<Dimension3> mesh_subdiv;
interp.ComputeSurfaceMesh(ref_cond, var.mesh, mesh_subdiv, var, 1);
// evaluating the solution x on quadrature points of the selected surfaces
VectComplex_wp trace_En, trace_Hn;
var.ComputeEnHnOnBoundary(interp, x, trace_En, trace_Hn);
return 0;
}
Location :
Harmonic/VarGeometryProblem.hxx
Harmonic/VarProblemInline.cxx
comm_group_mode
This attribute is the MPI communicator used to distribute the mesh over processors. By default, this communicator is set to MPI_COMM_WORLD such that a single computation is distributed over all nodes. If the computation is performed with several modes (for instance in an axisymmetric configuration), it may be interesting to compute each mode simultaneously. If you want that each mode is solved in sequential, you can set this communicator to MPI_COMM_SELF.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// each mode is solved on a single processor :
var.comm_group_mode = MPI_COMM_SELF;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to finish
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
GetNbMainUnknownDof
Syntax
| int GetNbMainUnknownDof() |
This method returns the number of degrees of freedom for the main unknown. For the HDG formulation, the main unknown is the volume unknown (such as u for acoustics).
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of degrees of freedom for u ?
int nb_ddl_u = var.GetNbMainUnknownDof();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetDofNumberOnElement
Syntax
| IVect GetDofNumberOnElement(int i, int num=0) |
This method returns the numbers of the degrees of freedom for the element i. By default, degrees of freedom are those of the first mesh numbering (num = 0). If there are several mesh numberings, you can provide the considered number.
Parameters
- i (in)
- element number
- num (optional)
- number of the mesh numbering
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// degrees of freedom for a given element
int num_elem = 15;
IVect Nodle = var.GetDofNumberOnElement(num_elem);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetScalarDofNumberOnElement
Syntax
| IVect GetScalarDofNumberOnElement(int i) |
This method returns the numbers of the degrees of freedom for the element i. For 3-D Maxwell's equations (and first-order formulation), it provides degrees of freedom for the physical unknown E and unknown E* (in PMLs).
Parameters
- i (in)
- element number
- num (optional)
- number of the mesh numbering
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// degrees of freedom for a given element
int num_elem = 15;
IVect Nodle = var.GetScalarDofNumberOnElement(num_elem);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbGlobalMeshDof
Syntax
| int GetNbGlobalMeshDof(int n = 0) |
This method returns the global number of degrees of freedom (by adding dofs of all processors) for a given mesh numbering. This number should be the same for any number of processors.
Parameters
- n (optional)
- number of the mesh numbering
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// local number of degrees of freedom for a mesh numbering (here only one mesh numbering exists for Helmholtz equation)
int nloc = var.GetNbMeshDof(); // this number is the degrees of freedom of the current processor
// global number of degrees of freedom (independant of the number of processors)
int nglob = var.GetNbGlobalMeshDof();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbGlobalDofPML
Syntax
| int GetNbGlobalDofPML(int n = 0) |
This method returns the global number of degrees of freedom (by adding dofs of all processors) for a given mesh numbering. This number should be the same for any number of processors. Here we count only degrees of freedom associated with PMLs.
Parameters
- n (optional)
- number of the mesh numbering
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// local number of degrees of freedom in PMLs for a mesh numbering (here only one mesh numbering exists for Helmholtz equation)
int nloc = var.GetMeshNumbering(0).GetNbDofPML(); // this number is the degrees of freedom of the current processor
// global number of degrees of freedom in PMLs (independant of the number of processors)
int nglob = var.GetNbGlobalDofPML();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbGlobalDof
Syntax
| int GetNbGlobalDof() const |
This method returns the global number of degrees of freedom for all the problem. It includes the degrees of freedom for all the unknowns and additional models. This number should be the same for any number of processors and correspdonds to the size of the finite element matrix in sequential.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// local number of degrees of freedom (i.e. size of the matrix)
int nloc = var.GetNbDof(); // this number is the degrees of freedom of the current processor
// global number of degrees of freedom (independant of the number of processors)
int nglob = var.GetNbGlobalDof();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbGlobalUnknownDof
Syntax
| int GetNbGlobalUnknownDof(int n = 0) |
This method returns the global number of degrees of freedom (by adding dofs of all processors) for a given unknown. This number should be the same for any number of processors.
Parameters
- n (optional)
- number of the unknown
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// local number of degrees of freedom for the unknown
int nloc = var.GetNbDofUnknown(0); // this number is the degrees of freedom of the current processor
// global number of degrees of freedom (independant of the number of processors)
int nglob = var.GetNbGlobalUnknownDof(0);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbGlobalCondensedDof
Syntax
| int GetNbGlobalCondensedDof(int n = 0) |
This method returns the global number of degrees of freedom (by adding dofs of all processors) for a given unknown after static condensation. Only dofs located on the boundaries of the elements are counted, interior dofs are condensed. This number should be the same for any number of processors.
Parameters
- n (optional)
- number of the unknown
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// local condensed number of degrees of freedom for the unknown
int nloc = var.GetOffsetDofCondensed(1) - var.GetOffsetDofCondensed(0); // this number is the degrees of freedom of the current processor
// global condensed number of degrees of freedom (independant of the number of processors)
int nglob = var.GetNbGlobalCondensedDof(0);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetOffsetGlobalUnknownDof
Syntax
| int GetOffsetGlobalUnknownDof(int n) |
This method returns the cumulated global number of degrees of freedom (by adding dofs of all processors) for a given unknown. This number should be the same for any number of processors.
Parameters
- n (in)
- number of the unknown
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// cumulated local number of degrees of freedom for the unknown 2
// this offset is useful to access to the correct row of the matrix
int offset_ loc = var.GetOffsetDofUnknown(2);
// cumulated global number of degrees of freedom (independant of the number of processors)
int offset_glob = var.GetOffsetGlobalUnknownDof(2);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetGlobalDofNumber
Syntax
| int GetGlobalDofNumber(int i) |
| const IVect& GetGlobalDofNumber() |
This method returns the global number of a local dof. You can also retrieve the array containing all the numbers.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// global dof number from the local dof :
int num_local = 13;
int num_global = var.GetGlobalDofNumber(num_local);
// all the array
const IVect& loc_to_glob = var.GetGlobalDofNumber();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbPointsQuadratureNeighbor
Syntax
| int GetNbPointsQuadratureNeighbor() const |
This method returns the number of quadrature points located on boundaries that are connected with elements that belong to other processors. This number can be used to estimate the cost of the communication.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of quadrature points on the interfaces with other processors ?
int nb_quad_neigh = var.GetNbPointsQuadratureNeighbor();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbSubdomains
Syntax
| int GetNbSubdomains() const |
This method does not return the number of subdomains (each subdomain being treated by a MPI process), but the number of subdomains that are connected to the current subdomain. It represents the number of neighboring subdomains.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of processors that will interact with the current one ?
int nb_proc_interac = var.GetNbSubdomains();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNbProcPerMode
Syntax
| int GetNbProcPerMode() const |
This method returns the number of processors involved in the computation of one mode. It is equal to the size of the MPI communicator comm_group_mode.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of processors involved in the computation
int nb_proc = var.GetNbProcPerMode();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetRankProcMode
Syntax
| int GetRankProcMode() const |
This method returns the rank ot the current processor involved in the computation of one mode. It is equal to the rank of the MPI communicator comm_group_mode.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of processors involved in the computation
int nb_proc = var.GetNbProcPerMode();
// rank of current processor ?
int rank_proc = var.GetRankProcMode();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetProcMatchingNeighbor
Syntax
| IVect& GetProcMatchingNeighbor() const |
This method returns the list of processors that have common degrees of freedom with the current processor.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// neighboring processors
const IVect& neighbor_proc = var.GetProcMatchingNeighbor();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetOriginalMatchingDofNeighbor
Syntax
| Vector<IVect>& GetOriginalMatchingDofNeighbor() const |
This method returns the degrees of freedom that are shared with other processors. The returned variable is an array of arrays, since there is a list of degrees of freedom for each processor (in the list given by GetProcMatchingNeighbor). The degrees of freedom are correctly sorted such that the dofs from processor p to processor q correspond to the dofs from processor q to processor p. These arrays are used to assemble a distributed vector.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// neighboring processors
const IVect& neighbor_proc = var.GetProcMatchingNeighbor();
// shared dofs
const Vector<IVect>& shared_dofs = var.GetOriginalMatchingDofNeighbor();
for (int i = 0; i < neighbor_proc.GetM(); i++)
{
int proc = neighbor_proc(i); // processor number
IVect local_dof = shared_dofs(i); // dofs shared with proc
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetElementNumberNeighboringFace
Syntax
| int GetElementNumberNeighboringFace(int num_face) |
This method returns the global number of the element adjacent to the neighboring face. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetOffsetNeighboringFace
Syntax
| int GetOffsetNeighboringFace(int num_face) |
This method returns the offset for quadrature points of a neighboring face. It corresponds to the cumulated number of quadrature points (from face 0 until face num_face-1) of neighboring faces only. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR. This offset is useful, when we want to store the solutions on quadrature points of the interface with other processors (in order to send/ receive values).
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// offset for quadrature points
int offset_neighbor = var.GetOffsetNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetProcessorNeighboringFace
Syntax
| int GetProcessorNeighboringFace(int num_face) |
This method returns the processor number of the element adjacent to the neighboring face. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// number of the another processor ?
int proc = var.GetProcessorNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetLocalPositionNeighboringFace
Syntax
| int GetLocalPositionNeighboringFace(int num_face) |
This method returns the local position of the face in the element adjacent to the neighboring face. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// local position of the face in the element ?
int num_loc = var.GetLocalPositionNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetRotationNeighboringFace
Syntax
| int GetRotationNeighboringFace(int num_face) |
This method returns the difference of orientation of the neighboring face. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// rotation of the face (between the two elements) ?
int rot = var.GetRotationNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetRefDomainNeighboringFace
Syntax
| int GetRefDomainNeighboringFace(int num_face) |
This method returns the reference of the element adjacent to the neighboring face. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// reference of this element
int ref_domain = var.GetRefDomainNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetTypeEltNeighboringFace
Syntax
| int GetTypeEltNeighboringFace(int num_face) |
This method returns the type of the element adjacent to the neighboring face. In 3-D, the type is equal to 0 for a tetrahedron, 1 for a pyramid, 2 for a wedge and 3 for an hexahedron. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// type of element
int type_elt = var.GetTypeEltNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetOrderEltNeighboringFace
Syntax
| int GetOrderEltNeighboringFace(int num_face, int n=0) |
This method returns the order of approximation of the element adjacent to the neighboring face. The order of approximation is the order associated with the mesh numbering n. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// order of approximation ?
int r = var.GetOrderEltNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetNodleNeighboringFace
Syntax
| IVect GetNodleNeighboringFace(int num_face, int n=0) |
This method returns the dof numbers of the element adjacent to the neighboring face. The order of approximation is the order associated with the mesh numbering n. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// global numbers of degrees of freedom of the adjacent element
IVect Nodle = var.GetNodleNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNodlePmlNeighboringFace
Syntax
| IVect GetNodlePmlNeighboringFace(int num_face, int n=0) |
This method returns the dof numbers (among PML dofs) of the element adjacent to the neighboring face. The order of approximation is the order associated with the mesh numbering n. The face num_face is assumed to be neighboring (i.e. there exists an element adjacent to this face that belongs to another processor than the current processor). In Montjoie, the neighboring faces have a fictitious boundary condition called LINE_NEIGHBOR.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// selecting a neighboring face
int num_face = 13;
int ref = var.mesh.Boundary(num_face).GetReference();
if (var.mesh.GetBoundaryCondition(ref) == BoundaryConditionEnum::LINE_NEIGHBOR)
{
// number of the element on the other side ?
int num_elem_glob = var.GetElementNumberNeighboringFace(num_face);
// global numbers of degrees of freedom of the adjacent element
IVect Nodle = var.GetNodleNeighboringFace(num_face);
// and numbers between PML dofs (significant if the element is inside PML)
IVect NodlePml = var.GetNodlePmlNeighboringFace(num_face);
}
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetSizeOffsetDofV
Syntax
| int GetSizeOffsetDofV() |
This method returns the size of the array storing offsets for vectorial dofs. Usually it is equal to nb_elt+1, where nb_elt is the number of elements in the mesh.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// nb_elt+1
int size_off_v = var.GetSizeOffsetDofV();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetOffsetDofV, SetOffsetDofV
Syntax
| int GetOffsetDofV(int i ) const |
| void SetOffsetDofV(int i , int offset ) |
The method GetOffsetDofV returns the offset for vectorial degrees of freedom. For continuous finite elements, when a mixed formulation is used, variables are continuous (such as the pressure for acoustics), whereas other variables are discontinuous (such as the velocity for acoustics). For discontinuous variables, no mesh numbering is performed, only an array storing the offsets is constructed. In this method, we return the offset for the given element. For HDG formulation, this array is used to store the offset for volume dofs whereas the mesh numbering is used only for surface dofs. The method SetOffsetDofV allows the user to change an offset. It should not be used in regular cases, since the array is already constructed in ComputeMeshAndFiniteElement.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// nb_elt+1
int size_off_v = var.GetSizeOffsetDofV();
// for a given element, first dof number for the vectorial dofs of the element
int num_eleme = 11;
int offset = var.GetOffsetDofV(num_elem);
// dofs of the element are offset + 3*j, offset + 3*j+1, offset+3*j+2
// where j is the local number (inside the element)
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetNbOverlappedDof
Syntax
| int GetNbOverlappedDof() const |
This method returns the number of degrees of freedom that belong to another processor. In Montjoie, the mesh is split into several subdomains (each subdomain being affected to a MPI process), such as degrees of freedom located at the interface are shared by several processors. For a shared degree of freedom, we consider that a main processor (usually the processor of lower rank) owns this dof, whereas it is an overlapped degree of freedom for the other processors.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of dofs already belonging to another processor
int nb_overlapped_dof = var.GetNbOverlappedDof();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetOverlappedDofNumber
Syntax
| int GetOverlappedDofNumber(int i ) const |
| const IVect& GetOverlappedDofNumber() const |
This method returns the list of degrees of freedom that belong to another processor. In Montjoie, the mesh is split into several subdomains (each subdomain being affected to a MPI process), such as degrees of freedom located at the interface are shared by several processors. For a shared degree of freedom, we consider that a main processor (usually the processor of lower rank) owns this dof, whereas it is an overlapped degree of freedom for the other processors. You can retrieve a single overlapped dof or all the list.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of dofs already belonging to another processor
int nb_overlapped_dof = var.GetNbOverlappedDof();
// loop over overlapped dofs
for (int i = 0; i < nb_overlapped_dof; i++)
{
int num_dof = var.GetOverlappedDofNumber(i); // dof number
}
// you can also retrieve the whole array
const IVect& dof_overlap = var.GetOverlappedDofNumber();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetOverlappedProcNumber
Syntax
| int GetOverlappedProcNumber(int i ) const |
| const IVect& GetOverlappedProcNumber() const |
This method returns the list of original processors that own overlapped degrees of freedom. In Montjoie, the mesh is split into several subdomains (each subdomain being affected to a MPI process), such as degrees of freedom located at the interface are shared by several processors. For a shared degree of freedom, we consider that a main processor (usually the processor of lower rank) owns this dof, whereas it is an overlapped degree of freedom for the other processors. With this method, you can have the number of the main processor (for all the dofs or for a single dof).
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// number of dofs already belonging to another processor
int nb_overlapped_dof = var.GetNbOverlappedDof();
// loop over overlapped dofs
for (int i = 0; i < nb_overlapped_dof; i++)
{
int num_dof = var.GetOverlappedDofNumber(i); // dof number
int proc = var.GetOverlappedProcNumber(i); // proc number
}
// you can also retrieve the whole arrays
const IVect& dof_overlap = var.GetOverlappedDofNumber();
const IVect& proc_overlap = var.GetOverlappedProcNumber();
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
AllocateDistributedVector
Syntax
| DistributedVector* AllocateDistributedVector(Vector& x ) const |
This method creates a new distributed vector and returns its adress. The distributed vector will contain the datas of the vector given as argument. To avoid duplicate memory releases (if you delete manually the pointer), it is advised to call NullifyDistributedVector. Distributed vectors are useful, if you need to compute scalar products (in order take into account overlapped dofs) or norms.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
VectComplex_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand(); y.FillRand();
// if you want to compute the scalar product (x, y), it is better to use distributed vectors (in parallel)
DistributedVector<Complex_wp>* x_par = var.AllocateDistributedVector(x);
DistributedVector<Complex_wp>* y_par = var.AllocateDistributedVector(y);
// x and *x_par point to the same data
Complex_wp scal = DotProd(*x_par, *y_par);
// to avoid deleting two times the same pointer, use Nullify
var.NullifyDistributedVector(x_par); // x_par is deleted properly by this method
var.NullifyDistributedVector(y_par); // y_par is deleted properly by this method
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
NullifyDistributedVector
Syntax
| void NullifyDistributedVector(DistributedVector* x ) const |
This method deletes a distributed vector without releasing the internal data contained in it.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
VectComplex_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand(); y.FillRand();
// if you want to compute the scalar product (x, y), it is better to use distributed vectors (in parallel)
DistributedVector<Complex_wp>* x_par = var.AllocateDistributedVector(x);
DistributedVector<Complex_wp>* y_par = var.AllocateDistributedVector(y);
// x and *x_par point to the same data
Complex_wp scal = DotProd(*x_par, *y_par);
// to avoid deleting two times the same pointer, use Nullify
var.NullifyDistributedVector(x_par); // x_par is deleted properly by this method
var.NullifyDistributedVector(y_par); // y_par is deleted properly by this method
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
SetEpartSplitting
Syntax
| void SetEpartSplitting(const IVect& epart ) const |
This method sets manually how the mesh is split into several subdomains for parallel computing. The array epart given as argument stores the processor number for each element. The recommended way to specify the algorithm used to split the mesh is to provide a line with SplitDomain in the datafile.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to set the array epart manually (to split the mesh in parallel)
int N = 1000; IVect epart(N); // N is the number of elements
int nb_proc = 3; // number of processors
for (int i = 0; i < N; i++)
epart(i) = i%nb_proc;
var.SetEpartSplitting(epart); // ComputeMeshAndFiniteElement will use the provided splitting
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
VectComplex_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand(); y.FillRand();
// if you want to compute the scalar product (x, y), it is better to use distributed vectors (in parallel)
DistributedVector<Complex_wp>* x_par = var.AllocateDistributedVector(x);
DistributedVector<Complex_wp>* y_par = var.AllocateDistributedVector(y);
// x and *x_par point to the same data
Complex_wp scal = DotProd(*x_par, *y_par);
// to avoid deleting two times the same pointer, use Nullify
var.NullifyDistributedVector(x_par); // x_par is deleted properly by this method
var.NullifyDistributedVector(y_par); // y_par is deleted properly by this method
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
SaveEpartSplitting
Syntax
| void SaveEpartSplitting( string file_name) const |
This method saves the array epart in a file. The array epart stores the processor number for each element. The recommended way to specify this file (if desired) is to provide a line with SaveSplitDomain in the datafile.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
VectComplex_wp x(var.GetNbDof()), y(var.GetNbDof());
x.FillRand(); y.FillRand();
// if you want to compute the scalar product (x, y), it is better to use distributed vectors (in parallel)
DistributedVector<Complex_wp>* x_par = var.AllocateDistributedVector(x);
DistributedVector<Complex_wp>* y_par = var.AllocateDistributedVector(y);
// x and *x_par point to the same data
Complex_wp scal = DotProd(*x_par, *y_par);
// to avoid deleting two times the same pointer, use Nullify
var.NullifyDistributedVector(x_par); // x_par is deleted properly by this method
var.NullifyDistributedVector(y_par); // y_par is deleted properly by this method
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetMemoryUsed
Syntax
| void GetMemoryUsed( map<string, size_t>& detail_mem) const |
This method fills the object detail_mem with the memory used by the different variables (jacobian matrices, mesh, etc).
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// if you want details about memory usage
map<string, size_t> detail_mem;
var.GetMemoryUsed(detail_mem);
// and display the memory usage stored in detail_mem :
var.DisplayMemoryUsed(detail_mem);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
DisplayMemoryUsed
Syntax
| void DisplayMemoryUsed( map<string, size_t>& detail_mem) const |
This method displays the memory usage as stored in the object detail_mem.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// if you want details about memory usage
map<string, size_t> detail_mem;
var.GetMemoryUsed(detail_mem);
// and display the memory usage stored in detail_mem :
var.DisplayMemoryUsed(detail_mem);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
GetNodleElement
Syntax
| IVect GetNodleElement(int i, int n = 0) const |
This method returns the number of the degrees of freedom of the element i. The second argument is optional and is the number of the mesh numbering.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// degrees of freedom of an element
int num_elem = 16;
IVect Nodle = var.GetNodleElement(num_elem);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
FindElementsInsidePML
Syntax
| void FindElementsInsidePML() |
This method updates elements such that elements in PMLs are marked as PML elements. This method is already called by ComputeMeshAndFiniteElement such that it does not need to be called in a regular use.
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
InitDistributedMatrix
Syntax
| void InitDistributedMatrix(DistributedMatrix& A) const |
This method initializes the distributed matrix to correspond to a finite element matrix (with the corrected shared rows). After calling this method, the matrix can be filled with methods such as AddInteraction, AddInteractionRow, AddDistanceInteraction.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
DistributedMatrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
// initialization of parallel stuff
var.InitDistributedMatrix(A);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblemInline.cxx
AddDomains
Syntax
| void AddDomains(Vector& x, int nb_u=-1) const |
This method assembles a vector, it is meaningful for a parallel computation and continuous finite elements. For continuous finite elements, the values of shared degrees of freedom are summed. As a result, the values of X on shared dofs coincide between processors.
Parameters
- x (inout)
- vector to assemble
- nb_u (optional)
- number of unknowns
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
VectComplex_wp feval, contrib;
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
// in parallel the contribution of elements must be added between processors (for shared dofs)
var.AddDomains(b);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ReduceDistributedVector
Syntax
| void ReduceDistributedVector(Vector& x, MPI_Op oper, int nb_u=-1, bool only_num=false) const |
This method reduces a vector, it is meaningful for a parallel computation and continuous finite elements. For continuous finite elements, the values of shared degrees of freedom are reduced, e.g. summed if oper is equal to MPI_SUM. As a result, the values of X on shared dofs coincide between processors.
Parameters
- x (inout)
- vector to reduce
- oper (in)
- reduction operation (MPI_SUM, MPI_MIN or MPI_MAX)
- nb_u (optional)
- number of unknowns
- only_num (optional)
- if true, we assume that there is only one mesh numbering
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
VectComplex_wp feval, contrib;
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
// in parallel the contribution of elements must be added between processors (for shared dofs) => AddDomains
// if you want another operation (max instead of the sum) => ReduceDistributedVector
var.ReduceDistributedVector(b, MPI_MAX);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
AssembleDirichlet
Syntax
| void AssembleDirichlet(Vector& x, int nb_u=-1, bool only_num=false) const |
This method assembles a vector for Dirichlet degrees of freedom, it is meaningful for a parallel computation and continuous finite elements. For continuous finite elements, the values of shared degrees of freedom (associated with Dirichlet condition) are summed.
Parameters
- x (inout)
- vector to assemble
- nb_u (optional)
- number of unknowns
- only_num (optional)
- if true, only one mesh numbering is considered
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
VectComplex_wp feval, contrib;
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
// if you want to sum values on Dirichlet dofs only
var.AssembleDirichlet(b);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ReduceDirichlet
Syntax
| void ReduceDirichlet(Vector& x, MPI_Op oper, int nb_u=-1, bool only_num=false) const |
This method reduces a vector for Dirichlet dofs, it is meaningful for a parallel computation and continuous finite elements. For continuous finite elements, the values of shared degrees of freedom (associated with Dirichlet condition) are reduced, e.g. summed if oper is equal to MPI_SUM.
Parameters
- x (inout)
- vector to reduce
- oper (in)
- reduction operation (MPI_SUM, MPI_MIN or MPI_MAX)
- nb_u (optional)
- number of unknowns
- only_num (optional)
- if true, we assume that there is only one mesh numbering
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
VectComplex_wp feval, contrib;
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
// if you want another operation for Dirichlet dofs
var.ReduceDirichlet(b, MPI_MAX);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ConstructDirichletComm
Syntax
| void ConstructDirichletComm() const |
This method updates arrays needed by the methods AssembleDirichlet or ReduceDirichlet. This method is already automatically called by ComputeMeshAndFiniteElement such that it does not need to be called in a regular use.
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ExchangeDomains
Syntax
| void ExchangeDomains(Vector& x, int nb_u=-1) const |
This method is meaningful for a parallel computation and continuous finite elements. For continuous finite elements, the values of shared degrees of freedom are exchanged. This method is used when each degree of freedom is shared by at most two processors. For a dof shared by two processors, the value on the first processor is exchanged with the value on the second processor.
Parameters
- x (inout)
- vector whose values are exchanged
- nb_u (optional)
- number of unknowns
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// to compute the right hand side manually, you can add contributions of each element
VectComplex_wp b(var.GetNbDof()); b.Zero();
VectComplex_wp feval, contrib;
SetPoints<Dimension3> pts; VectR3 s; VectComplex_wp feval, contrib;
for (int i = 0; i < var.mesh.GetNbElt(); i++)
{
bool affine = var.mesh.IsElementAffine(i);
var.mesh.GetVerticesElement(i, s);
const ElementReference_Dim<Dimension3>& Fb = var.GetReferenceElement(i);
Fb.FjElemQuadrature(s, pts, var.mesh, i);
feval.Reallocate(Fb.GetNbPointsQuadratureInside());
contrib.Reallocate(Fb.GetNbDof());
for (int j = 0; j < Fb.GetNbPointsQuadratureInside(); j++)
feval(j) = var.GetWeightedJacobian(i, j, affine, Fb)*exp(-Norm2(pts.GetPointQuadrature(i)));
Fb.ApplyCh(feval, contrib);
var.AddLocalUnknownVector(1.0, contrib, i, b);
}
// if you want to exchange values between processors
var.ExchangeDomains(b);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ExchangeRelaxDomains
Syntax
| void ExchangeRelaxDomains(Vector& x, Real_wp omega, int proc, int nb_u=-1) const |
This method is meaningful for a parallel computation and continuous finite elements. The processor ranked proc sends its values (on shared degrees of freedom to other processors). The following operation is done for processors that receive the values
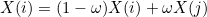
where X(j) is the value sent by the processor proc.
Parameters
- x (inout)
- vector whose values are exchanged
- omega (in)
- relaxation parameter
- proc (in)
- rank of the processor that sends the values
- nb_u (optional)
- number of unknowns
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// starting from random values (different values on each processor)
VectComplex_wp b(var.GetNbDof()); b.FillRand();
// if you want to send values of processor 1 to other processors
// other processors store these new values with a relaxation (to keep a part of old values)
Real_wp omega = 0.5;
var.ExchangeRelaxDomains(b, omega, 1);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ExchangeQuadRelaxDomains
Syntax
| void ExchangeQuadRelaxDomains(Vector& x, Real_wp omega, int proc, int nb_u=-1) const |
This method is meaningful for a parallel computation and continuous finite elements. The processor ranked proc sends its values (on shared quadrature points to other processors). The following operation is done for processors that receive the values
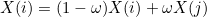
where X(j) is the value sent by the processor proc.
Parameters
- x (inout)
- vector whose values are exchanged
- omega (in)
- relaxation parameter
- proc (in)
- rank of the processor that sends the values
- nb_u (optional)
- number of unknowns
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// starting from random values (different values on each processor)
VectComplex_wp b(var.GetNbPointsQuadratureNeighbor()); b.FillRand();
// if you want to send values of processor 1 to other processors
// other processors store these new values with a relaxation (to keep a part of old values)
Real_wp omega = 0.5;
var.ExchangeQuadRelaxDomains(b, omega, 1);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ExchangeUfaceDomains
Syntax
| void ExchangeUfaceDomains( | const Vector& x, Vector& xsend, Vector& xsend_tmp, |
| Vector& xrecv, Vector& xrecv_tmp, Vector<MPI_Request>& request, int tag) const |
This method is meaningful for a parallel computation. The values on quadrature points of the interfaces (between subdomains, each processor owning a subdomain) are exchanged. The exchange is achieved when the method GetUfaceDomains is called. The separation in two methods is made in the purpose of overlapping communications with computations.
Parameters
- x (inout)
- vector whose values are exchanged
- xsend (out)
- temporary vectors
- xsend_tmp (out)
- temporary vectors
- xrecv (out)
- temporary vectors
- xrecv_tmp (out)
- temporary vectors
- request (out)
- MPI requests
- tag (in)
- tag number used in MPI communications
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// starting from random values (different values on each processor)
VectComplex_wp b(var.GetNbPointsQuadratureNeighbor()); b.FillRand();
// if you want to exchange values with the corresponding processor
// first step : initialize the non-blocking communications
Vector<VectComplex_wp> xsend, xrecv;
Vector<Vector<int64_t> > xsend_tmp, xrecv_tmp;
Vector<MPI_Request> request; int tag = 17;
var.ExchangeUfaceDomains(b, xsend, xsend_tmp, xrecv, xrecv_tmp, request, tag);
// then you can overlap communications with computational tasks
Complex_wp scal = DotProd(b, b);
// and complete the echange with GetUfaceDomains
var.GetUfaceDomains(b, xsend, xsend_tmp, xrecv, xrecv_tmp, request, tag);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetUfaceDomains
Syntax
| void ExchangeUfaceDomains( | Vector& x, Vector& xsend, Vector& xsend_tmp, |
| Vector& xrecv, Vector& xrecv_tmp, Vector<MPI_Request>& request, int tag) const |
This method is meaningful for a parallel computation. The values on quadrature points of the interfaces (between subdomains, each processor owning a subdomain) are exchanged. The exchange is initialized when the method ExchangeUfaceDomains is called. The separation in two methods is made in the purpose of overlapping communications with computations.
Parameters
- x (inout)
- vector whose values are exchanged
- xsend (out)
- temporary vectors
- xsend_tmp (out)
- temporary vectors
- xrecv (out)
- temporary vectors
- xrecv_tmp (out)
- temporary vectors
- request (out)
- MPI requests
- tag (in)
- tag number used in MPI communications
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// starting from random values (different values on each processor)
VectComplex_wp b(var.GetNbPointsQuadratureNeighbor()); b.FillRand();
// if you want to exchange values with the corresponding processor
// first step : initialize the non-blocking communications
Vector<VectComplex_wp> xsend, xrecv;
Vector<Vector<int64_t> > xsend_tmp, xrecv_tmp;
Vector<MPI_Request> request; int tag = 17;
var.ExchangeUfaceDomains(b, xsend, xsend_tmp, xrecv, xrecv_tmp, request, tag);
// then you can overlap communications with computational tasks
Complex_wp scal = DotProd(b, b);
// and complete the echange with GetUfaceDomains
var.GetUfaceDomains(b, xsend, xsend_tmp, xrecv, xrecv_tmp, request, tag);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ReduceDistributedVectorFace
Syntax
| void ReduceDistributedVectorFace(Vector& x, MPI_Op oper, int nb_u=1) const |
This method reduces a vector, it is meaningful for a parallel computation. Instead of considering shared degrees of freedom (as for ), we consider shared faces (edges in 2-D).
Parameters
- x (inout)
- vector to reduce
- oper (in)
- reduction operation (MPI_SUM, MPI_MIN or MPI_MAX)
- nb_u (optional)
- number of unknowns
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// if you want to save the computed splitting in a file
var.SaveEpartSplitting("epart.dat"); // ComputeMeshAndFiniteElement will save the computed splitting in the file epart.dat
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
var.ComputeQuasiPeriodicPhase(); // for quasi-periodic conditions
// we consider a coefficient for each face of the mesh
VectReal_wp coef_face(var.mesh.GetNbBoundary()); coef_face.Zero();
// loop over faces to compute it
for (int i = 0; i < var.mesh.GetNbBoundary(); i++)
{
// any quantity
coef_face(i) += 1.0;
}
// you can assemble the values between processors (shared faces will have 2.0 with the given example)
var.ReduceDistributedVectorFace(coef_face, MPI_MAX);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
ComputeLocalProlongation
Syntax
| void ComputeLocalProlongation(FiniteElementInterpolator& proj, DistributedProblem& var_coarse, int rc, TinyVector<Matrix<Real_wp>, 4>& PrologationElement) const |
This method computes the prolongation operator (as needed by multigrid algorithms) between a coarse problem and the current problem (considered as a fine problem).
Parameters
- proj (out)
- projector from the coarse element to the fine element
- var_coarse (in)
- coarse problem
- rc (in)
- order of approximation for the coarse problem
- ProlongationElement (out)
- prolongation matrices (if stored)
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// definition of the coarse problem
EllipticProblem<HarmonicElasticEquation<Dimension3> > var_coarse;
var_coarse.InitIndices(100); var_coarse.SetTypeEquation(type_equation);
ReadInputFile("test_coarse.ini", var_coarse);
var_coarse.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var_coarse.PerformOtherInitializations(); // other initializations
var_coarse.ComputeMassMatrix();
// prolongation operator
FiniteElementInterpolator proj; TinyVector<Matrix<Real_wp>, 4> ProlongationElement;
var.ComputeLocalProlongation(proj, var_coarse, var_coarse.GetMeshNumbering(0).GetOrder(),
ProlongationElement);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
Harmonic/DistributedProblem.cxx
GetNewEllipticProblem
Syntax
| DistributedProblem* GetNewEllipticProblem() const |
This virtual method constructs an object of the leaf class EllipticProblem and returns the address of the created object. It can be used mainly for generic functions (in order to use polymorphism instead of templating).
Example :
// instead of templating with the equation, we can template only with the dimension
// => less instantations
template<class Dimension>
void MyGenericFunction(DistributedProblem<Dimension> var_fine)
{
// to create a coarse problem for example
DistributedProblem<Dimension>* var_coarse = var_fine.GetNewEllipticProblem();
// complete the function
// the object can be deleted normally
delete var_coarse;
}
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// we call the function
MyGenericFunction(var);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
CopyFiniteElement
Syntax
| void CopyFiniteElement(const DistributedProblem& var) const |
This virtual method copies the finite elements from another class. The copy is a shallow copy, only pointers are copied. As a result, if the object given as argument is cleared, the finite elements will not point to the correct addresses.
Example :
int main()
{
EllipticProblem<HarmonicElasticEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
EllipticProblem<HarmonicElasticEquation<Dimension3> > varb;
// if you want to copy input data
varb.CopyInputData(var);
// and finite elements
varb.CopyFiniteElement(var);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
ComputeEnHnNodal
Syntax
| void ComputeEnHnNodal( | Vector<Vector>& u_nodal , Vector<Vector>& grad_nodal , int num_elem, const VectR_N& pts , |
| const VectR_N& normale, Vector<Vector>& En_nodal , Vector<Vector>& Hn_nodal ) const |
This virtual method computes the trace of the solution (E x n for Maxwell's equations, u for Helmholtz) and of its gradient (H x n for Maxwell, du/dn for Helmholtz). Since this notion depends on the equation, the method is virtual and overloaded correctly on the leaf class.
Parameters
- u_nodal (in)
- values of the solution on nodal points
- grad_nodal (in)
- gradient (curl for edge elements) of the solution on nodal points
- num_elem (in)
- element number
- pts (in)
- nodal points
- normale (in)
- outgoing normales
- En_nodal (out)
- E x n on nodal points
- Hn_nodal (out)
- H x n on nodal points
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// let&s assume that you computed a solution
VectComplex_wp xsol(var.GetNbDof());
xsol.FillRand();
// we extract values on degrees of freedom for a given element
int num_elem = 12;
Vector<VectComplex_wp> u_loc(1);
var.GetLocalUnknownVector(xsol, num_elem, u_loc);
// computing nodal points and jacobian matrices
VectR3 s; var.mesh.GetVerticesElement(num_elem, s);
const ElementReference<Dimension3, 2> Fb = var.GetReferenceElementHcurl(num_elem);
SetPoints<Dimension3> PointsElem; SetMatrices<Dimension3> MatricesElem;
Fb.FjElemNodal(s, PointsElem, var.mesh, num_elem);
Fb.DFjElemNodal(s, PointsElem, MatricesElem, var.mesh, i);
// nodal points and normales on the surface
int num_loc = 3; Real_wp dsj; Matrix3_3 dfjm1;
int nb_nodes_surf = Fb.GetNbNodalBoundary(num_loc);
VectR3 pts(nb_nodes_surf), normale(nb_nodes_surf);
for (int i = 0; i < nb_nodes_surf; i++)
{
int n = Fb.GetNodalNumber(num_loc, i);
pts(i) = PointsElem.GetPointNodal(n);
GetInverse(MatricesElem.GetPointNodal(n), dfjm1);
Fb.GetNormale(dfjm1, normale(i), dsj, num_loc);
}
// we compute nodal values (here grad_nodal is the curl of E on nodal points)
Vector<VectComplex_wp> u_nodal, du_nodal, grad_nodal;
Fb.ComputeNodalValues(MatricesElem, u_loc, u_nodal, var.mesh, num_elem);
Fb.ComputeNodalGradient(MatricesElem, u_nodal, du_nodal);
Fb.GetCurlFromGradient(du_nodal, grad_nodal);
// nodal values on the surface
Vector<VectComplex_wp> u_nodal_surf(3), grad_nodal_surf(3);
for (int i = 0; i < 3; i++)
{
Fb.ComputeValueNodalBoundary(u_nodal(i), u_nodal_surf(i), num_elem, num_loc);
Fb.ComputeValueNodalBoundary(grad_nodal(i), grad_nodal_surf(i), num_elem, num_loc);
}
Vector<VectComplex_wp> En_nodal, Hn_nodal;
var.ComputeEnHnNodal(u_nodal_surf, grad_nodal_surf, num_elem, pts, normale, En_nodal, Hn_nodal);
return 0;
}
Location :
Harmonic/DistributedProblem.hxx
ComputeDofCoordinates
Syntax
| void ComputeDofCoordinates(VectR_N& points_dof) |
This method computes the coordinates for all the degrees of freedom of the main unknown. This method works only for interpolation finite elements (such as QUADRANGLE_LOBATTO). For hp elements, it does not work.
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// coordinates of degrees of freedom ?
VectR3 PointsDof;
var.ComputeDofCoordinates(PointsDof);
return 0;
}
Location :
Harmonic/VarProblem.hxx
Harmonic/VarProblem.cxx
ComputeReferenceGradientElement
Syntax
| void ComputeReferenceGradientElement(int i, const VectReal_wp& u_dof, const VectReal_wp& u_quad, VectReal_wp& grad_u) |
This method computes the gradient (on the reference element) of a field u from components on degrees of freedom. For some finite elements (that compute the gradient from values of quadrature points), you have to provide the value of u on quadrature points. To obtain the gradient on the real element, the transformation Fi has to be taken into account.
Parameters
- i (in)
- element number
- u_dof (in)
- values of the field on degress of freedom of the selected element
- u_quad (in)
- values of the field on quadrature points
- grad_u (out)
- gradient of the field (on the reference element)
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// for a given element
int num_elem = 12;
const ElementReference<Dimension3, 1>& Fb = var.GetReferenceElementH1(num_elem);
VectReal_wp u_dof(Fb.GetNbDof()); u_dof.FillRand();
VectReal_wp u_quad(Fb.GetNbPointsQuadratureInside());
// computing the values on quadrature points
Fb.ApplyChTranspose(u_dof, u_quad);
// and gradient (on the reference element) on quadrature points
VectReal_wp grad_u(3*Fb.GetNbPointsQuadratureInside());
var.ComputeReferenceGradientElement(i, u_dof, u_quad, grad);
return 0;
}
Location :
Harmonic/VarProblem.hxx
Harmonic/VarProblem.cxx
GetMassMatrixType
Syntax
| int GetMassMatrixType(VectBool& diag_elt) |
This method returns the nature of the mass matrix. The output argument contains the elements where the mass matrix is diagonal (if there is partial mass lumping). The different types are contained in the class FemMassMatrix, and can be equal to :
- DIAGONAL : the mass matrix is diagonal.
- BLOCK_DIAGONAL_UNSYM : the mass matrix is block-diagonal.
- DIAG_MATRIX_FREE : the mass matrix is partially diagonal (a part of elements are lumped) .
- BLOCK_DIAG_MATRIX_FREE : the mass matrix is partially block-diagonal (a part of elements are lumped with vectorial dofs) .
- MATRIX_FREE : the mass matrix does not need to be stored (default case) .
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// nature of the mass matrix ?
VectBool diag_elt;
int nature = var.GetMassMatrixType(diag_elt);
if (nature == FemMassMatrix::DIAGONAL)
cout << "Diagonal mass matrix" << endl;
// if nature is equal to DIAG_MATRIX_FREE, diag_elt(i) is true if the element i is lumped
return 0;
}
Location :
Harmonic/VarProblem.hxx
Harmonic/VarProblem.cxx
GetElementaryMatrixType
Syntax
| int GetElementaryMatrixType() |
This method returns 0 if the elementary matrix is dense, 1 if it is sparse. Some finite elements (usually lumped elements in 3-D) produce sparse elementary matrices.
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// nature of the elementary matrix
int nature = var.GetElementaryMatrixType();
if (nature == 1)
cout << "Sparse elementary matrix" << endl;
return 0;
}
Location :
Harmonic/VarProblem.hxx
Harmonic/VarProblem.cxx
ComputeEnHnQuadrature
Syntax
| void ComputeEnHnQuadrature( | Vector<Vector>& u_quadrature , Vector<Vector>& grad_quadrature , int num_elem, const VectR_N& pts , |
| const VectR_N& normale, bool compute_H, Vector<Vector>& En_quad , Vector<Vector>& Hn_quad ) const |
This virtual method computes the trace of the solution (E x n for Maxwell's equations, u for Helmholtz) and of its gradient (H x n for Maxwell, du/dn for Helmholtz). Since this notion depends on the equation, the method is virtual and overloaded correctly on the leaf class.
Parameters
- u_quadrature (in)
- values of the solution on quadrature points
- grad_quadrature (in)
- gradient (curl for edge elements) of the solution on quadrature points
- num_elem (in)
- element number
- pts (in)
- quadrature points
- normale (in)
- outgoing normales
- compute_H (in)
- if false, only E x n is computed
- En_quad (out)
- E x n on quadrature points
- Hn_quad (out)
- H x n on quadrature points
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// then the mesh and finite element are constructed
var.ComputeMeshAndFiniteElement("HEXAHEDRON_LOBATTO");
var.PerformOtherInitializations(); // other initializations
var.ComputeMassMatrix(); // computation of geometric quantities (such as jacobian matrices)
// let&s assume that you computed a solution
VectComplex_wp xsol(var.GetNbDof());
xsol.FillRand();
// we extract values on degrees of freedom for a given element
int num_elem = 12;
Vector<VectComplex_wp> u_loc(1);
var.GetLocalUnknownVector(xsol, num_elem, u_loc);
// computing quadrature points and jacobian matrices
VectR3 s; var.mesh.GetVerticesElement(num_elem, s);
const ElementReference<Dimension3, 2> Fb = var.GetReferenceElementHcurl(num_elem);
SetPoints<Dimension3> PointsElem; SetMatrices<Dimension3> MatricesElem;
Fb.FjElemQuadrature(s, PointsElem, var.mesh, num_elem);
Fb.DFjElemQuadrature(s, PointsElem, MatricesElem, var.mesh, i);
// quadrature points and normales on the surface
int num_loc = 3; Real_wp dsj; Matrix3_3 dfjm1;
Fb.FjSurfaceElem(s, PointsElem, var.mesh, num_elem, num_loc);
Fb.DFjSurfaceElem(s, PointsElem, MatricesElem, var.mesh, num_elem, num_loc);
int nb_pts_quad = Fb.GetNbQuadBoundary(num_loc);
VectR3 pts(nb_pts_quad), normale(nb_pts_quad);
// computation of E (and curl E) on quadrature points of the surface
VectComplex_wp Equad_ref(3*nb_pts_quad), curlEquad_ref(3*nb_pts_quad);
Fb.ApplyShTranspose(num_loc, u_loc(0), Equad_ref);
Fb.ApplyNablaShTranspose(num_loc, u_loc(0), curlEquad_ref);
// application of Piola transform
Vector<VectComplex_wp> Equad(3), curlE_quad(3);
for (int k = 0; k < 3; k++)
{
Equad(k).Reallocate(nb_pts_quad);
curlE_quad(k).Reallocate(nb_pts_quad);
}
Matrix3_3 dfj, dfjm1; R3_Complex_wp Eref, curlEref, Et, curlEt;
for (int i = 0; i < nb_pts_quad; i++)
{
dfj = MatricesElem.GetPointQuadratureBoundary(i);
jacob = Det(dfj);
pts(i) = PointsElem.GetPointQuadratureBoundary(i);
normale(i) = MatricesElem.GetNormaleQuadratureBoundary(i);
Eref.Init(Equad_ref(3*i), Equad_ref(3*i+1), Equad_ref(3*i+2));
curlEref.Init(curlEquad_ref(3*i), curlEquad_ref(3*i+1), curlEquad_ref(3*i+2));
GetInverse(dfj, dfjm1);
MltTrans(dfjm1, Eref, Et);
Mlt(dfj, curlEref, curlEt); Mlt(1.0/jacob, curlEt);
Equad(0)(i) = Et(0); Equad(1)(i) = Et(1); Equad(2)(i) = Et(2);
curlE_quad(0)(i) = curlEt(0); curlE_quad(1)(i) = curlEt(1); curlE_quad(2)(i) = curlEt(2);
}
// computation of E x n and H x n from values on quadrature points
VectComplex_wp En_quad, Hn_quad;
var.ComputeEnHnQuadrature(Equad, curlE_quad, num_elem, pts, normale, true, En_quad, Hn_quad);
return 0;
}
Location :
Restart
Syntax
| void Restart() |
This method reinitializes some attributes such that a computation can be restarted
Example :
EllipticProblem<HelmholtzEquationDG<Dimension3> > var;;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// allocating the arrays for physical indexes
var.InitIndices(100); // we choose N = 100
var.SetTypeEquation(type_equation);
// then you can read the data file
ReadInputFile("test.ini", var);
// the mesh and finite elements are constructed
var.ComputeMeshAndFiniteElement(type_element);
// then other initializations (if needed)
var.PerformOtherInitializations();
// if you want to use the same object to run another simulation
var.Restart();
// then the simulation is completed as usual
ReadInputFile("test2.ini", var);
var.ComputeMeshAndFiniteElement(type_element);
var.PerformOtherInitializations();
// etc
Location :
ConstructAll
Syntax
| void ConstructAll( | string input_file , string name_elt , string name_eq, All_LinearSolver*& solver , |
| bool compute_rho=true, bool delete_pts=true, int num=-1) |
This method constructs all what is needed to compute finite element matrices. It can be useful in order to avoid calling the same sequence of methods (ReadInputFile, ComputeMeshAndFiniteElement, ComputeMassMatrix, etc).
Parameters
- input_file (in)
- name of the data file
- name_elt (in)
- name of the finite element
- name_eq (in)
- name of the equation
- solver (out)
- linear solver to use for the factorization of the finite element matrix
- compute_rho (optional)
- if true, physical indexes are computed
- delete_pts (optional)
- if true, quadrature points are not stored
- num (optional)
- simulation number
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// then you can compute finite element matrices
GlobalGenericMatrix<Complex_wp> nat_mat;
Matrix<Complex_wp, Symmetric, ArrayRowSymSparse> A;
var.AddMatrixWithBC(A, nat_mat);
// or factorize a finite element matrix
solver->PerformFactorizationStep(nat_mat);
// and solve the linear system A x = b
VectComplex_wp b(var.GetNbDof()), x; b.FillRand();
x = b; solver->ComputeSolution(x);
// when you no longer need the solver, you can release the memory
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
RunAll
Syntax
| void RunAll( | string input_file , string name_elt , string name_eq int num=-1) |
This method runs the complete simulation :
- constructs the mesh and finite element
- compute the solutions for the required right hand sides
- writes the solution on the asked outputs
Parameters
- input_file (in)
- name of the data file
- name_elt (in)
- name of the finite element
- name_eq (in)
- name of the equation
- num (optional)
- simulation number
Example :
int main()
{
EllipticProblem<HarmonicMaxwellEquation_3D > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing and solving the problem
var.RunAll("test.ini", type_element, type_equation);
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetInverseSquareRootMassMatrix
Syntax
| void GetInverseSquareRootMassMatrix( | Vector& Dh ) |
This method computes the matrix
 where Dh is the mass matrix of the considered equation. For example, it is equal to
where Dh is the mass matrix of the considered equation. For example, it is equal to
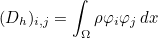
for Laplace equation. It works only if mass lumped elements are used (with Gauss-Lobatto points), such that the mass matrix is diagonal.
Example :
int main()
{
EllipticProblem<LaplaceEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// then you can compute Dh^{-1/2} where Dh is the mass matrix
VectReal_wp invDh_sqrt;
var.GetInverseSquareRootMassMatrix(invDh_sqrt);
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetMassMatrix
Syntax
| void GetMassMatrix( | Vector& Dh , bool assemble=true) |
This method computes the mass matrix Dh of the considered equation. For example, it is equal to
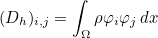
for Laplace equation. It works only if mass lumped elements are used (with Gauss-Lobatto points), such that the mass matrix is diagonal. If the second argument (optional) is equal to false, the mass matrix is not assembled (between processors).
Example :
int main()
{
EllipticProblem<LaplaceEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// then you can compute the mass matrix Dh
VectReal_wp Dh;
var.GetMassMatrix(Dh);
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
SetComputationFarPoints
Syntax
| void SetComputationFarPoints( | VectR_N& points, Real_wp dt) |
This method provides to the object the points outside the computational domain where the solution should be computed. For some equations, an integral representation is used in order to compute the solution on these points. The second argument is the time step (used for unsteady problems). These points are usually provided by inserting a line with SismoOutsidePoints in the datafile.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetNewTransparentSolver
Syntax
| TransparencySolver_Base* GetNewTransparentSolver( | All_LinearSolver& solver) |
This method creates a new transparent solver and returns the address of the created object. The transparent solver allows to compute the solution with a transparent condition by iterating with solutions with first-order absorbing conditions (by using integral representations). The transparent solver manages this iterative process.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// we factorize the finite element matrix
GlobalGenericMatrix<Complex_wp> nat_mat;
solver->PerformFactorizationStep(nat_mat);
// we solve the linear system A x = b
VectComplex_wp source_rhs(var.GetNbDof()), x_sol; source_rhs.FillRand();
x_sol = source_rhs; solver->ComputeSolution(x_sol);
// retrieving a transparent solver
TransparencySolver_Base* solv_transp = var.GetNewTransparentSolver(*solver);
if (solv_transp->UseTransparentCondition())
{
solv_transp->Init(); // initialization step
source_rhs = x_sol;
solv_transp->Solve(x_sol, source_rhs); // iterative solver to find the solution with the transparent condition
}
delete solv_transp;
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetNewEigenSolver
Syntax
| EigenProblemMontjoie<T>* GetNewEigenSolver( | All_LinearSolver& solver, T x) |
This method creates a new eigenvalue solver and returns the address of the created object. The eigenvalue solver allows to compute eigenvalues and eigenvectors of the considered problem. The second argument is used to select a complex (or real) eigensolver.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// retrieving an eigenvalue solver
EigenProblemMontjoie<Real_wp>* eigen_solver = var.GetNewEigenSolver(*solver, Real_wp(0));
ReadInputFile("test.init", *eigen_solver); // parameters of the data file
if (eigen_solver->GetNbAskedEigenvalues() > 0)
eigen_solver->ComputeEigenModes();
delete eigen_solver;
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetNewPolynomialEigenSolver
Syntax
| PolynomialEigenProblemMontjoie<T>* GetNewPolynomialEigenSolver( | All_LinearSolver& solver, T x) |
This method creates a new polynomial eigenvalue solver and returns the address of the created object. The polynomial eigenvalue solver allows to compute eigenvalues and eigenvectors of the considered problem. The second argument is used to select a complex (or real) eigensolver. For some equations (and for specific media), the eigenvalue problem can be set as a polynomial eigenproblem (instead of a linear eigenproblem).
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// retrieving an eigenvalue solver
PolynomialEigenProblemMontjoie<Real_wp>* eigen_solver = var.GetNewPolynomialEigenSolver(*solver, Real_wp(0));
ReadInputFile("test.init", *eigen_solver); // parameters of the data file
if (eigen_solver->GetNbAskedEigenvalues() > 0)
eigen_solver->ComputeEigenModes();
delete eigen_solver;
delete solver;
return 0;
}
Location :
Harmonic/VarHarmonicBase.hxx
Harmonic/VarHarmonicBase.cxx
GetGenericImpedanceFunction
Syntax
| ImpedanceGeneric& GetGenericImpedanceFunction() |
This method returns the object handling impedance boundary conditions.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// retrieving the object to compute impedance coefficients
ImpedanceGeneric<Complex_wp, HelmholtzEquation<Dimension3> >& imped = var.GetGenericImpedanceFunction();
return 0;
}
Location :
Harmonic/VarHarmonic.hxx
Harmonic/VarHarmonicInline.cxx
GetAbsorbingImpedanceFunction
Syntax
| ImpedanceABC& GetAbsorbingImpedanceFunction() |
This method returns the object handling absorbing boundary conditions.
Example :
int main()
{
EllipticProblem<HelmholtzEquation<Dimension3> > var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
VectR3 pts3d(1); pts3d(0).Init(-100.0, 0.0, 0.0);
var.SetComputationFarPoints(pts3d, 0.0);
// constructing the problem
All_LinearSolver* solver; // the pointer solver will be initialized in ConstructAll
var.ConstructAll("test.ini", type_element, type_equation, solver);
// retrieving the object to compute impedance coefficients for absorbing boundary conditions
ImpedanceABC<Complex_wp, HelmholtzEquation<Dimension3> >& imped = var.GetAbsorbingImpedanceFunction();
return 0;
}
Location :
Harmonic/VarHarmonic.hxx
Harmonic/VarHarmonicInline.cxx
fct_impedance_absorbing
Syntax
| ImpedanceABC<Complexe, TypeEquation> fct_impedance_absorbing |
This attribute stores the object that computes impedance coefficients for absorbing boundary conditions.
Location :
fct_impedance_generic
Syntax
| ImpedanceGeneric<Complexe, TypeEquation> fct_impedance_generic |
This attribute stores the object that computes impedance coefficients for impedance boundary conditions.
Location :
fct_impedance_high_conduc
Syntax
| ImpedanceHighConductivity<Complexe, TypeEquation> fct_impedance_high_conduc |
This attribute stores the object that computes impedance coefficients for high conductivtiy boundary conditions.
Location :
output_rcs_param
Syntax
| VarComputationRCS<TypeEquation> output_rcs_param |
This attribute stores the object that computes radar cross sections (RCS).
Location :
var_transmission
Syntax
| VarTransmission<TypeEquation> var_transmission |
This attribute stores the object that implements transmission conditions (equivalent models).
Location :
var_gibc
Syntax
| VarGeneralizedImpedance<TypeEquation> var_gibc |
This attribute stores the object that implements generalized impedance boundary conditions (GIBC).
Location :
GetFourierMode
Syntax
| void GetFourierMode(Real_wp teta , T& val) |
If val is a complex number, it is set to
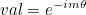
where m is the current mode number. If val is a real number, it is set to
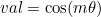
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// treating the first mode :
var.SetCurrentModeNumber(var.GetModeNumber(0));
// value e^{-i m theta} for this mode ?
Complex_wp val; Real_wp teta = 0.1;
var.GetFourierMode(teta, val);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
IsVertexOnAxis
Syntax
| bool IsVertexOnAxis(int i) |
This method returns true if the vertex i is located on the axis of revolution (x = 0).
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// treating the first mode :
var.SetCurrentModeNumber(var.GetModeNumber(0));
// vertex 3 on the axis of revolution ?
bool vert_on_axis = var.IsVertexOnAxis(3);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
IsElementNearAxis
Syntax
| bool IsElementNearAxis(int i) |
This method returns true if the element i is located on the axis of revolution (x = 0). An element located on the axis has at least one vertex on the axis.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// treating the first mode :
var.SetCurrentModeNumber(var.GetModeNumber(0));
// element 3 close to the axis ?
bool elt_on_axis = var.IsElementNearAxis(3);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
NumberOfModesToBeComputed
Syntax
| bool NumberOfModesToBeComputed() |
This method returns true if the number of Fourier modes has to be computed automatically (by evaluating right hand sides and stopping as soon as the right hand side is small enough). It corresponds to a line NumberModes = AUTO 1e-6 in the data file.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// do we have to compute the number of modes ?
bool mode_auto = var.NumberOfModesToBeComputed();
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
GetModeThreshold
Syntax
| Real_wp GetModeThreshold() |
This method returns the threshold used to compute the number of Fourier modes. It corresponds to the second parameter of a line NumberModes = AUTO 1e-6 in the data file.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// do we have to compute the number of modes ?
bool mode_auto = var.NumberOfModesToBeComputed();
// threshold to drop modes ?
Real_wp eps = var.GetModeThreshold();
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
GetBessel_Value
Syntax
| Real_wp GetBessel_Value(int n , int num_point ) |
This method returns the Bessel function Jn(k r) for a given quadrature point.
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblemInline.cxx
CheckSectionMeshAxi
Syntax
| void CheckSectionMeshAxi() |
This method checks that the mesh contains only elements with x > 0, such that it is compatible with an axisymmetric configuration. It also finds elements close to the axis. This method is called by CheckInputMesh such that it does not need to be called in a regular use.
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
ComputeDofOnAxe
Syntax
| void ComputeDofOnAxe(VarProblem& var) |
This method computes the numbers of the degrees of freedom located on the axis. This method is called by PerformOtherInitializations such that it does not need to be called in a regular use.
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
Get_KwavePerp_Kz_Phase
Syntax
| static void Get_KwavePerp_Kz_Phase( | Complex_wp rho, Complex_wp mu, int m, R3 kwave, Real_wp omega, |
| Real_wp& k_perp, Real_wp& kz, bool& incidence_axial, Complex_wp& phase) |
This method computes the following quantities
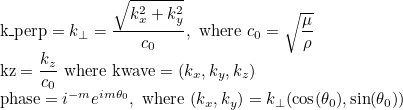
It is useful to decompose a plane wave into Fourier modes. incidence_axial is true if the wave vector is oriented along z-axis.
Parameters
- rho (in)
- physical index (as introduced in Helmholtz equation)
- mu(in)
- physical index (as introduced in Helmholtz equation)
- m (in)
- mode number
- kwave (in)
- wave vector
- omega (in)
- pulsation
- k_perp (out)
- transverse wave number
- kz (out)
- longitudinal wave number
- incidence_axial (out)
- true if k_perp is small enough
- phase (out)
- i-m ei m θ0
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// for a given wave vector
R3 kwave(1, 2, -1); Real_wp omega = Norm2(kwave);
// we want to compute k_perp, k_z and phase
Real_wp k_perp, kz; bool incidence_axial; Complex_wp phase;
int m = 2; Complex_wp rho(1, 0), mu(1, 0);
var.Get_KwavePerp_Kz_Phase(rho, mu, m, kwave, omega, k_perp, kz, incidence_axial, phase);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
ComputeNbModes_Generic
Syntax
| void ComputeNbModes_Generic( | Real_wp kt) |
This method computes the number of modes needed to compute accurately the Jacobi-Anger expansion

This expansion is used to decompose an incident plane wave into Fourier modes, since
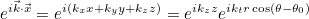
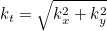
is the transverse wave number. The methods returns the integer M, such that the user should consider modes between -M and M to have an accurate solution with the given transverse wave number. The precision is given with the method GetModeThreshold.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// for a given wave vector
R3 kwave(1, 2, -1); Real_wp omega = Norm2(kwave);
// we want to compute k_perp, k_z and phase
Real_wp k_perp, kz; bool incidence_axial; Complex_wp phase;
int m = 2; Complex_wp rho(1, 0), mu(1, 0);
var.Get_KwavePerp_Kz_Phase(rho, mu, m, kwave, omega, k_perp, kz, incidence_axial, phase);
// number of modes for an incident plane wave with kwave ?
int M = var.ComputeNbModes_Generic(k_perp);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
ComputeListMode
Syntax
| void ComputeListMode( | VarComputationRCS_Axi& rcs_param) |
This method computes the number of modes needed to compute accurately the radar cross section (RCS) given as parameter. It calls successively ComputeNbModes_Generic for the difference incident angles to obtain a maximum number of modes.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// object containing datas about radar cross section
VarComputationRCS_Axi rcs_param(var);
ReadInputFile("test.ini", rcs_param);
var.InitRcs(rcs_param);
// number of modes needed to evaluate rcs ?
int M = var.ComputeListMode(rcs_param);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
InitRcs
Syntax
| void InitRcs( | VarComputationRCS_Axi rcs_param) |
This method initializes the computation of radar cross section.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// object containing datas about radar cross section
VarComputationRCS_Axi rcs_param(var);
ReadInputFile("test.ini", rcs_param);
var.InitRcs(rcs_param);
// number of modes needed to evaluate rcs ?
int M = var.ComputeListMode(rcs_param);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
GetNbRightHandSide
Syntax
| int GetNbRightHandSide( | VarComputationRCS_Axi rcs_param) |
This method returns the number of right hand sides needed to compute the radar cross section.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// object containing datas about radar cross section
VarComputationRCS_Axi rcs_param(var);
ReadInputFile("test.ini", rcs_param);
var.InitRcs(rcs_param);
// number of modes needed to evaluate rcs ?
int M = var.ComputeListMode(rcs_param);
// number of sources (plane waves) ?
int nb_rhs = var.GetNbRightHandSide(rcs_param);
return 0;
}
Location :
Harmonic/VarAxisymProblem.hxx
Harmonic/VarAxisymProblem.cxx
InitBesselArray
Syntax
| void InitBesselArray( | VarComputationRCS_Axi rcs_param) |
This method precomputes Bessel functions Jn(k r) for the incident plane waves contained in rcs_param. The aim is to obtain an efficient computation of the right hand sides, by using recurrence relations on Bessel functions.
Example :
int main()
{
EllipticProblem<HelmholtzEquationAxi> var;
// we retrieve the type of finite element and equation in the data file
string type_element, type_equation;
getElement_Equation("test.ini", type_element, type_equation);
// constructing the problem
Vector<string> lines_data_file;
var.ConstructAll("test.ini", type_element, lines_data_file);
var.ComputeMassMatrix();
// object containing datas about radar cross section
VarComputationRCS_Axi rcs_param(var);
ReadInputFile("test.ini", rcs_param);
var.InitRcs(rcs_param);
// number of modes needed to evaluate rcs ?
int M = var.ComputeListMode(rcs_param);
// number of sources (plane waves) ?
int nb_rhs = var.GetNbRightHandSide(rcs_param);
// precomputing Bessel functions
var.InitBesselArray(rcs_param);
// then Jn can be retrieved with GetBessel_Value
int nb_pts_quad = rcs_param.GetInterpolationMesh().GetNbAllQuadraturePoints();
int num_angle = 3, k = 10; // num_angle : number of the plane wave, k : number of the quadrature point
int m = 1; int num_point = num_angle*nb_pts_quad + k;
Real_wp evalJn = var.GetBessel_Value(m, num_point);
return 0;
}