Other classes associated with meshes
We detail the class NumberMap which is used to store the number of degrees of freedom per vertex, edge, triangle, tetrahedron, etc. The finite element class will fill an object of type NumberMap with the method ConstructNumberMap, then the mesh is able to number mesh with the method NumberMesh. We also detail the class ElementNumbering which stores the degrees of freedom of an element. This class is used in the class MeshNumbering.
Methods for ElementNumbering
| GetMemorySize | returns the memory used by the object in bytes |
| GetNbDof | returns the number of degrees of freedom of the element |
| GetNumberDof | returns dof number of a degree of freedom |
| GetNodle | returns all dof numbers |
| GetNegativeDofNumber | returns dof numbers of dofs having a different sign globally and locally |
| SetNegativeDofNumber | sets dof numbers of dofs having a different sign globally and locally |
| ReallocateDof | sets the number of degree of freedoms contained in the element |
| SetNumberDof | sets dof number of a degree of freedom contained in the element |
| AddDof | changes the number of degree of freedoms contained in the element |
| PushDof | adds a dof at the end of list |
| Clear | removes information about degrees of freedom |
| ReallocateFaces | changes the number of faces |
| GetOrderFace | returns order of approximation of a face of the element |
| SetOrderFace | modifies order of approximation of a face of the element |
| GetOffsetFace | returns first dof number of a face of the element |
Methods of NumberMap
| GetMemorySize | returns the memory used by the object in bytes |
| GetDofNumberOnElement | retrieves dof numbers associated with an element of the mesh |
| GetLocalUnknownVector | extracts the local components of u on an element of the mesh |
| AddLocalUnknownVector | adds a local (with only values on degrees of freedom of an element of the mesh) vector to the global vector |
| ModifyLocalColumnMatrix | modifies the columns of the elementary matrix with respect to orientations and signs of global dofs |
| ModifyLocalRowMatrix | modifies the rows of the elementary matrix with respect to orientations and signs of global dofs |
| ModifyLocalComponentVector | intermediary function used by GetLocalUnknownVector |
| ModifyLocalUnknownVector | intermediary function used by AddLocalUnknownVector |
| GetGlobalUnknownVector | modification of local projection on reference element to obtain a global projection (respecting signs and orientations of global dofs) |
| GetNbDofVertex | returns the number of dofs per vertex |
| GetNbDofEdge | returns the number of dofs per edge |
| GetNbDofTriangle | returns the number of dofs per triangle |
| GetNbDofQuadrangle | returns the number of dofs per quadrangle |
| GetNbDofTetrahedron | returns the number of dofs per tetrahedron |
| GetNbDofPyramid | returns the number of dofs per pyramid |
| GetNbDofWedge | returns the number of dofs per wedge |
| GetNbDofHexahedron | returns the number of dofs per hexahedron |
| SetNbDofVertex | sets the number of dofs per vertex |
| SetNbDofEdge | sets the number of dofs per edge |
| SetNbDofTriangle | sets the number of dofs per triangle |
| SetNbDofQuadrangle | sets the number of dofs per quadrangle |
| SetNbDofTetrahedron | sets the number of dofs per tetrahedron |
| SetNbDofPyramid | sets the number of dofs per pyramid |
| SetNbDofWedge | sets the number of dofs per wedge |
| SetNbDofHexahedron | sets the number of dofs per hexahedron |
| GetNbDofElement | returns the number of dofs per element |
| SetOrder | fills numbering scheme with the numbers of dofs for a classical nodal finite element |
| GetSymmetricEdgeDof | returns dof number after symmetry of the edge |
| IsSkewSymmetricEdgeDof | returns true is this dof of the edge is skew-symmetric |
| SetOppositeEdgesDofSymmetry | tells that when the edge is symmetrized, dof numbers on the edge are reverted (case of nodal finite elements) |
| SetEqualEdgesDofSymmetry | tells that when the edge is symmetrized, dof numbers on the edge do not change (case of hp finite elements with symmetric and skew-symmetric dofs on the edges) |
| SetEdgesDofSymmetry | gives dof number on the edge after symmetry |
| SetSkewSymmetryEdgesDof | defines which dofs on the edges are skew-symmetric, and which dofs are symmetric |
| SetAllEdgesDofToSkewSymmetric | tells that all the dofs on the edges are skew-symmetric |
| SetOddEdgesDofToSkewSymmetric | tells that odd dofs on the edges are skew-symmetric |
| SetEvenEdgeDofToSkewSymmetric | tells that even dofs on the edges are skew-symmetric |
| DofInvariantByRotation | returns true if dofs of a face are invariant by rotation |
| SetFacesDofRotationTri | sets dof numbers after a rotation of a triangular face |
| SetFacesDofRotationQuad | sets dof numbers after a rotation of a quadrangular face |
| SetSignDofRotationTri | sets signs of dofs after a rotation of a triangular face |
| SetSignDofRotationQuad | sets signs of dofs after a rotation of a quadrangular face |
| IsNegativeDof | returns true if the dof has changed its sign after a rotation of the face |
| GetRotationFaceDof | returns dof number after a rotation of the face |
| GetNbPointsQuadBoundary | returns the number of quadrature points on all the faces of an element |
| GetQuadraturePoint | returns a quadrature point on the unit interval, unit triangle or unit square |
| ConstructQuadrature2D | construction of quadrature rules for unit interval |
| ConstructQuadrature3D | construction of quadrature rules for unit triangle and unit square |
| GetEdgeQuadrature | returns the quadrature points for the unit interval |
| GetTriangleQuadrature | returns the quadrature points for the unit triangle |
| GetQuadrangleQuadrature | returns the quadrature points for the unit square |
| SetPointsQuadratureTriangle | sets the quadrature points to use for the unit triangle |
| SetPointsQuadratureQuadrangle | sets the quadrature points to use for the unit square |
| SetPointsQuadratureEdge | sets the quadrature points to use for the unit interval |
| SetFluxWeightEdge | sets the quadrature half-weights for the unit interval |
| SetFluxWeightTriangle | sets the quadrature half-weights for the unit triangle |
| SetFluxWeightQuadrangle | sets the quadrature half-weights for the unit square |
| GetFluxWeight | returns the half-weights for an edge or face of the mesh |
| GetRotationQuadraturePoints | returns the quadrature points of a face after rotation |
| GetGmshTriangularNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for a triangle |
| GetGmshQuadrilateralNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for a quadrangle |
| GetGmshTetrahedralNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for a tetrahedron |
| GetGmshPyramidalNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for a pyramid |
| GetGmshPrismaticNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for a prism |
| GetGmshHexahedralNumbering | computes the array for the correspondance between Montjoie nodes and Gmsh nodes for an hexahedron |
| GetGmshEntityNumber | returns the Gmsh's entity number for an element of the mesh |
| FormulationDG | returns true if the finite element is associated with a discontinuous Galerkin formulation |
| SetFormulationDG | sets if the finite element is associated with a discontinuous Galerkin formulation |
| Clear | empties the object |
GetNbDofVertex
Syntax
| int GetNbDofVertex(int order) const |
This method returns the number of dofs per vertex.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; // we construct a finite element TriangleClassical tri; tri.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tri.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per vertex cout << "Number of dofs per vertex " << mesh_num.number_map.GetNbDofVertex(order);
Location :
GetNbDofEdge
Syntax
| int GetNbDofEdge(int order) const |
This method returns the number of dofs per edge. We take into account only internal dofs associated with the edge and not dofs associated with the vertices.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; // we construct a finite element TriangleClassical tri; tri.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tri.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per edge cout << "Number of dofs per edge " << mesh_num.number_map.GetNbDofEdge(order);
Location :
GetNbDofTriangle
Syntax
| int GetNbDofTriangle(int order) const |
This method returns the number of dofs per triangle. We take into account only internal dofs associated with the triangle and not dofs associated with the edges or vertices of the triangle.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; // we construct a finite element TriangleClassical tri; tri.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tri.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display the number of dofs per triangle cout << "Number of dofs per triangle " << mesh_num.number_map.GetNbDofTriangle(order);
Location :
GetNbDofQuadrangle
Syntax
| int GetNbDofQuadrangle(int order) const |
This method returns the number of dofs per quadrangle. We take into account only internal dofs associated with the quadrangle and not dofs associated with edges or vertices.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; // we construct a finite element QuadrangleLobatto quad; quad.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; quad.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per quadrangle cout << "Number of dofs per quadrangle " << mesh_num.number_map.GetNbDofQuadrangle(order);
Location :
GetNbDofTetrahedron
Syntax
| int GetNbDofTetrahedron(int order) const |
This method returns the number of dofs per tetrahedron. We take into account only internal dofs associated with the tetrahedron and not dofs associated with the faces, edges or vertices.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per tetrahedron cout << "Number of dofs per tetrahedron " << mesh_num.number_map.GetNbDofTetrahedron(order);
Location :
GetNbDofPyramid
Syntax
| int GetNbDofPyramid(int order) const |
This method returns the number of dofs per pyramid. We take into account only internal dofs associated with the pyramid and not dofs associated with the faces, edges or vertices.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element PyramidClassical elt; elt.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; elt.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per pyramid cout << "Number of dofs per pyramid " << mesh_num.number_map.GetNbDofPyramid(order);
Location :
GetNbDofWedge
Syntax
| int GetNbDofWedge(int order) const |
This method returns the number of dofs per wedge. We take into account only internal dofs associated with the wedge (triangular prism) and not dofs associated with the faces, edges or vertices.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element WedgeClassical elt; elt.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; elt.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of dofs per wedge cout << "Number of dofs per wedge " << mesh_num.number_map.GetNbDofWedge(order);
Location :
GetNbDofHexahedron
Syntax
| int GetNbDofHexahedron(int order) const |
This method returns the number of dofs per hexahedron. We take into account only internal dofs associated with the hexahedron and not dofs associated with the faces, edges or vertices.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element HexahedronLobatto elt; elt.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; elt.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display the number of dofs per hexahedron cout << "Number of dofs per hexahedron " << mesh_num.number_map.GetNbDofHexahedron(order);
Location :
GetSymmetricEdgeDof
Syntax
| int GetSymmetricEdgeDof(int order, int k) const |
This method returns the dof number of an edge after symmetry of this edge. This is used in NumberMesh when local orientation of the edge is the opposite of the global orientation. If you wish a more detailed explanation, you can look at SetEdgesDofSymmetry.
Example :
MeshNumbering<Dimension3> mesh_num(mesh);
int order = 3;
// we construct a finite element
TetrahedronClassical tet;
tet.ConstructFiniteElement(order);
// then number_map
int dg_form = ElementReference_Base::CONTINUOUS;
tet.ConstructNumberMap(mesh_num.number_map, dg_form);
// and display symmetric dofs
for (int k = 0; k < mesh_num.number_map.GetNbDofEdge(); k++)
cout << "Symmetric of dof " << k << " = " <<
mesh_num.number_map.GetSymmetricEdgeDof(order, k) << endl;
Location :
IsSkewSymmetricEdgeDof
Syntax
| bool IsSkewSymmetricEdgeDof(int order, int k) const |
This method returns true if the dof of an edge is skew-symmetric, i.e. the dof number doesn't change after symmetry of the edge, but since the basis function is antisymmetric, the sign changes. If you wish a more detailed explanation, you can look at SetEdgesDofSymmetry.
Example :
MeshNumbering<Dimension3> mesh_num(mesh);
int order = 3;
// we construct a finite element
TetrahedronClassical tet;
tet.ConstructFiniteElement(order);
// then number_map
int dg_form = ElementReference_Base::CONTINUOUS;
tet.ConstructNumberMap(mesh_num.number_map, dg_form);
// and display antisymmetric dofs
for (int k = 0; k < mesh_num.number_map.GetNbDofEdge(); k++)
if (mesh_num.number_map.IsSkewSymmetricEdgeDof(order, k))
cout << "Antisymmetric dof " << k << endl;
Location :
GetNbDofElement
Syntax
| int GetNbDofElement(int order, const Edge& elt) const |
| int GetNbDofElement(int order, const Face& elt) const |
| int GetNbDofElement(int order, const Volume& elt) const |
This method returns the number of dofs associated with the interior of the given element (which can be an edge, a face or a volume).
Example :
MeshNumbering<Dimension3> mesh_num(mesh);
int order = 3;
// we construct a finite element
TetrahedronClassical elt;
elt.ConstructFiniteElement(order);
// then number_map
int dg_form = ElementReference_Base::CONTINUOUS;
elt.ConstructNumberMap(mesh_num.number_map, dg_form);
// you can display number of dofs "to be placed" inside each element
for (int i = 0; i < mesh.GetNbElt(); i++)
cout << "Number of dofs inside element " <<
mesh_num.number_map.GetNbDofElement(order, mesh.Element(i)) << endl;
// you can display number of dofs "to be placed" inside each face :
for (int i = 0; i < mesh.GetNbBoundary(); i++)
cout << "Number of dofs inside face " <<
mesh_num.number_map.GetNbDofElement(order, mesh.Boundary(i)) << endl;
Location :
SetOrder
Syntax
| void SetOrder(const Mesh& mesh, int order) |
This method sets the number of dofs as for a classical nodal finite element :
- one dof per vertex
- (r-1) dofs per edge
- (r-1)(r-2)/2 dofs per triangle
- (r-1)(r-2)(r-3)/6 dofs per tetrahedron
- (r-1)(r-2)(2 r-3)/6 dofs per pyramid
- (r-1)(r-1)(r-2)/2 dofs per wedge
- (r-1)(r-1)(r-1) dofs per hexahedron
where r is the given order.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; mesh_num.SetOrder(order); // filling number_map with classical choice mesh_num.number_map.SetOrder(mesh, order); // the mesh can be numbered mesh_num.NumberMesh();
Location :
SetNbDofVertex
Syntax
| void SetNbDofVertex(int order, int nb_dof) const |
This method sets the number of dofs per vertex.
Example :
int order = 1; NumberMap nmap; // one dof per vertex (P1) nmap.SetNbDofVertex(order, 1);
Location :
SetNbDofEdge
Syntax
| void SetNbDofEdge(int order, int nb_dof) const |
This method sets the number of degrees of freedom associated with the inside of an edge.
Example :
int order = 1; NumberMap nmap; nmap.SetNbDofVertex(order, 1); // no dof on edges (like for P1) nmap.SetNbDofEdge(order, 0);
Location :
SetNbDofTriangle
Syntax
| void SetNbDofTriangle(int order, int nb_dof) const |
This method sets the number of dofs per triangle (interior of the triangle).
Example :
int order = 3; NumberMap nmap; // example of P3 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 2); nmap.SetNbDofTriangle(order, 1);
Location :
SetNbDofQuadrangle
Syntax
| void SetNbDofQuadrangle(int order, int nb_dof) const |
This method sets the number of dofs per quadrangle (only interior).
Example :
int order = 3; NumberMap nmap; // example of P3/Q3 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 2); nmap.SetNbDofTriangle(order, 1); nmap.SetNbDofQuadrangle(order, 4);
Location :
SetNbDofTetrahedron
Syntax
| void SetNbDofTetrahedron(int order, int nb_dof) const |
This method sets the number of dofs per tetrahedron (interior only).
Example :
int order = 4; NumberMap nmap; // example of P4 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); nmap.SetNbDofTriangle(order, 3); nmap.SetNbDofTetrahedron(order, 1);
Location :
SetNbDofPyramid
Syntax
| void SetNbDofPyramid(int order, int nb_dof) const |
This method sets the number of dofs per pyramid (interior only).
Example :
int order = 4; NumberMap nmap; // example of P4 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); nmap.SetNbDofTriangle(order, 3); nmap.SetNbDofQuadrangle(order, 9); nmap.SetNbDofTetrahedron(order, 1); nmap.SetNbDofPyramid(order, 5);
Location :
SetNbDofWedge
Syntax
| void SetNbDofWedge(int order, int nb_dof) const |
This method sets the number of dofs per wedge (interior only).
Example :
int order = 4; NumberMap nmap; // example of P4 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); nmap.SetNbDofTriangle(order, 3); nmap.SetNbDofQuadrangle(order, 9); nmap.SetNbDofTetrahedron(order, 1); nmap.SetNbDofPyramid(order, 5); nmap.SetNbDofWedge(order, 9);
Location :
SetNbDofHexahedron
Syntax
| void SetNbDofHexahedron(int order, int nb_dof) const |
This method sets the number of dofs per hexahedron.
Example :
int order = 4; NumberMap nmap; // example of P4 nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); nmap.SetNbDofTriangle(order, 3); nmap.SetNbDofQuadrangle(order, 9); nmap.SetNbDofTetrahedron(order, 1); nmap.SetNbDofPyramid(order, 5); nmap.SetNbDofWedge(order, 9); nmap.SetNbDofHexahedron(order, 27);
Location :
FormulationDG
Syntax
| int FormulationDG() const |
This method returns the type of discontinuous formulation associated with the numbering (ElementReference_Base::CONTINUOUS, ElementReference_Base::DISCONTINUOUS or ElementReference_Base::HDG)
Example :
int order = 3; NumberMap nmap; nmap.SetFormulationDG(ElementReference_Base::DISCONTINUOUS); if (nmap.FormulationDG() == ElementReference_Base::DISCONTINUOUS) cout << "DG Formulation used " << endl;
Location :
SetFormulationDG
Syntax
| void SetFormulationDG(int dg_form) |
You can store the type of discontinuous formulation in this object by calling this method. The parameter dg_form can be equal to ElementReference_Base::CONTINUOUS, ElementReference_Base::DISCONTINUOUS or ElementReference_Base::HDG.
Example :
int order = 3; NumberMap nmap; nmap.SetFormulationDG(ElementReference_Base::HDG); if (nmap.FormulationDG() == ElementReference_Base::HDG) cout << "HDG Formulation used " << endl;
Location :
SetOppositeEdgesDofSymmetry
Syntax
| void SetOppositeEdgesDofSymmetry(int order, int nb_dof) |
When you call this method, you tell that dofs numbers on the edge have to be symmetrized after a symmetry of the edge. This is the case for nodal finite elements, since dof numbers 0, 1, 2, 3 will be transformed into 3, 2, 1, 0 after a symmetry of the edge. For more details, look at SetEdgesDofSymmetry.
Example :
int order = 3; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 2); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 2);
Location :
SetEqualEdgesDofSymmetry
Syntax
| void SetEqualEdgesDofSymmetry(int order, int nb_dof) |
When you call this method, you tell that dofs numbers on the edge remain the same after a symmetry of the edge. This is the case for hp finite elements, since dof numbers 0, 1, 2, 3 will remain unchanged 0, 1, 2, 3 after a symmetry of the edge, only signs of some dofs are modified. By default, we consider that the sign of odd dofs is changed whereas the sign of even dofs is not changed. This is the case of Legendre polynomials used in hp finite elements. For more details, look at SetEdgesDofSymmetry.
Example :
int order = 3; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 2); // you give again the number of degrees of freedom on the edge nmap.SetEqualEdgesDofSymmetry(order, 2);
Location :
SetEdgesDofSymmetry
Syntax
| void SetEdgesDofSymmetry(int order, int i, int j, bool skew_sym) |
You can call this method after an initial call to SetOppositeEdgesDofSymmetry. You provide dof numbers after a symmetry of the edge, then you can also provide the possible changes of signs with method SetSkewSymmetryEdgesDof. When general meshes are considered, it is necessary to know the traces of basis functions on the edges when we change the orientation of the edge. For H1 finite elements, two classical finite elements are available in Montjoie, nodal finite elements and hp finite elements. For nodal finite elements, we have plotted the trace of basis functions associated with the edge on the figure below.
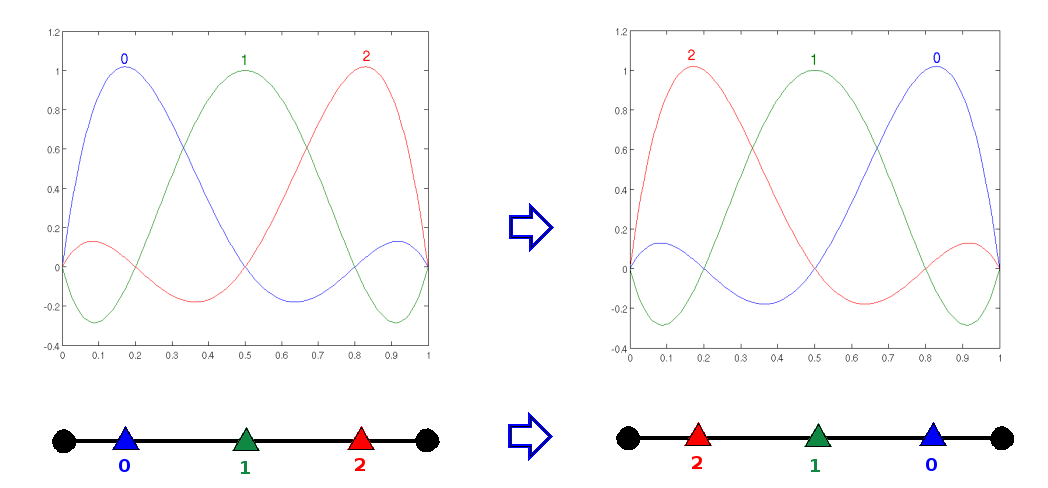
In this plot, we show the original trace and the trace after symmetry. We can see that the dofs 0, 1, 2 are transformed into dofs 2, 1, 0 and no change of signs is made. In order to provide this information to NumberMap, we call the method SetOppositeEdgesDofSymmetry.
For hp finite elements, the trace of basis functions are orthogonal polynomials (for example Legendre polynomials), which are plotted in the figure below.
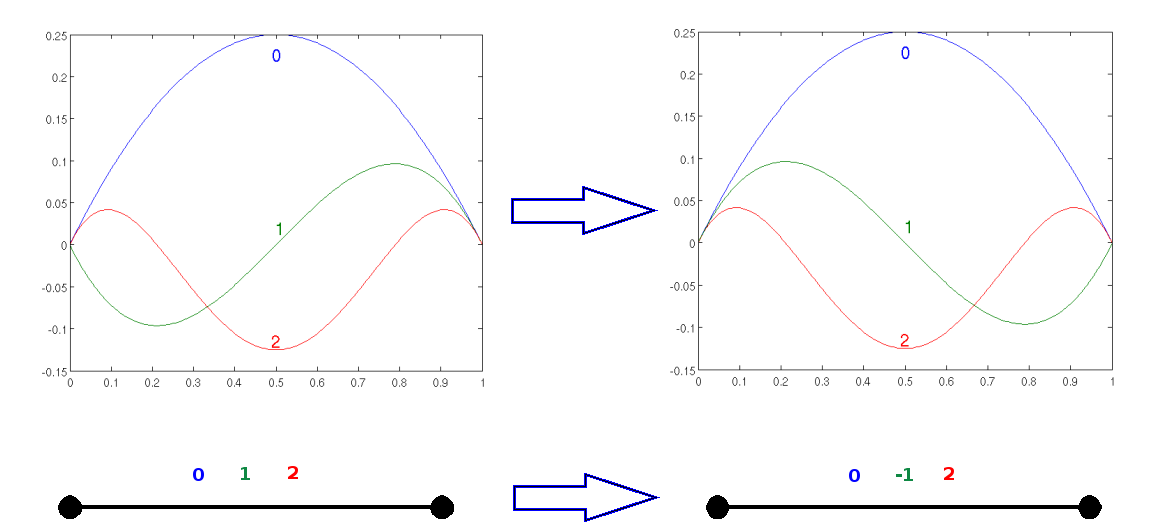
As you can see, the trace of these basis functions is symmetric (even Legendre polynomials) or antisymmetric (odd Legendre polynomials). As a result, dof numbers are unchanged but the sign of odd dof numbers is changed. In order to provide this information to NumberMap, we call the method SetEqualEdgesDofSymmetry.
If your finite element class has other properties, you can specify dof numbers and changement of signs manually with this method.
Parameters
- order (in)
- order of approximation
- i (in)
- dof number
- j (in)
- dof number after symmetry
- skew_sym (in)
- if true the sign of the basis function changes after symmetry
Example :
int order = 4; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 3); // if you want you can provide another dof numbers // for example, [0,1,2] can be transformed into [0, 2, 1] // and if there are changes of sign or no nmap.SetEdgesDofSymmetry(order, 0, 0, false); nmap.SetEdgesDofSymmetry(order, 1, 2, true); nmap.SetEdgesDofSymmetry(order, 2, 1, false);
Location :
SetSkewSymmetryEdgesDof
Syntax
| void SetSkewSymmetryEdgesDof(int order, const VectBool& sign) |
This method sets the change of signs for dofs associated with edge after symmetry. For each dof, if the value is true, the dof changes its sign (antisymmetric basis function), if the value is false, the dof remains unchanged (symmetric basis functions).
Example :
int order = 4; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 3); // if you want you can provide another dof numbers // for example, [0,1,2] can be transformed into [0, 2, 1] nmap.SetEdgesDofSymmetry(order, 0, 0, false); nmap.SetEdgesDofSymmetry(order, 1, 2, false); nmap.SetEdgesDofSymmetry(order, 2, 1, false); // you provide changes of sign (if any) Vector<bool> change_sign(3); change_sign.Fill(false); // for example, you can tell that only dof 1 will change its sign change_sign(1) = true; nmap.SetSkewSymmetryEdgesDof(order, change_sign);
Location :
SetAllEdgesDofToSkewSymmetric
Syntax
| void SetAllEdgesDofToSkewSymmetric(int order) |
This methods informs that all dofs associated with the edges are antisymmetric, and sign of dofs will change if the orientation of the local edge is different from the orientation of global edge.
Example :
int order = 4; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 3); // you can tell that all dofs are antisymmetric nmap.SetAllEdgesDofToSkewSymmetric(order);
Location :
SetOddEdgesDofToSkewSymmetric
Syntax
| void SetOddEdgesDofToSkewSymmetric(int order) |
This methods informs that odd dofs (1, 3, 5, 7, etc) associated with the edges are antisymmetric, and sign of odd dofs will change if the orientation of the local edge is different from the orientation of global edge.
Example :
int order = 4; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 3); // you can tell that odd dofs are antisymmetric nmap.SetOddEdgesDofToSkewSymmetric(order);
Location :
SetEvenEdgesDofToSkewSymmetric
Syntax
| void SetEvenEdgesDofToSkewSymmetric(int order) |
This methods informs that even dofs (0, 2, 4, 6, etc) associated with the edges are antisymmetric, and sign of even dofs will change if the orientation of the local edge is different from the orientation of global edge.
Example :
int order = 4; NumberMap nmap; nmap.SetNbDofVertex(order, 1); nmap.SetNbDofEdge(order, 3); // you give again the number of degrees of freedom on the edge nmap.SetOppositeEdgesDofSymmetry(order, 3); // you can tell that even dofs are antisymmetric nmap.SetEvenEdgesDofToSkewSymmetric(order);
Location :
DofInvariantByRotation
Syntax
| bool DofInvariantByRotation(int order, const Face<Dimension3> f) |
This method returns true if the dofs of the face f are invariant by rotation. A change of sign is however permitted. If the dofs are not invariant, there will be a non-trivial linear operator involved to project the rotated dofs to the original dofs.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element TetrahedronHierarchic tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // if you want to know if a face will need a linear operator // to be applied if it is rotated int num_face = 42; bool inv = mesh_num.number_map.DofInvariantByRotation(order, mesh.Boundary(num_face));
Location :
SetFacesDofRotationTri
Syntax
| void SetFacesDofRotationTri(int order, Matrix<int>& num) |
| void SetFacesDofRotationTri(int order, Vector<Matrix<Real_wp> >& oper_lin) |
When you call this method you provide the dof numbers obtained after a rotation of a triangular face. If you want more details about the different orientations of a triangular face, you can look at the method GetRotationFaceDof. If the dofs are not invariant by rotation, you can provide the linear operator to apply for each rotation (second syntax).
Example :
int order = 4; NumberMap nmap; // 3 dofs inside the triangle nmap.SetNbDofTriangle(order, 3); // you provide the dof numbers after rotation // if you are using nodal elements, there are useful methods in class MeshNumbering VectR2 Points2D(3); Points2D(0) = R2(0.2, 0.2); Points2D(1) = R2(0.8, 0.2); Points2D(2) = R2(0.2, 0.8); Matrix<int> num; MeshNumbering<Dimension3>::GetRotationTriangularFace(Points2D, num); // you provide this array to nmap nmap.SetFacesDofRotationTri(order, num);
Location :
SetFacesDofRotationQuad
Syntax
| void SetFacesDofRotationQuad(int order, Matrix<int>& num) |
| void SetFacesDofRotationQuad(int order, Vector<Matrix<Real_wp> >& oper_lin) |
When you call this method you provide the dof numbers obtained after a rotation of a quadrilateral face. If you want more details about the different orientations of a quadrilateral face, you can look at the method GetRotationFaceDof. If the dofs are not invariant by rotation, you can provide the linear operator to apply for each rotation (second syntax).
Example :
int order = 4; NumberMap nmap; // 4 dofs inside the quadrangle nmap.SetNbDofQuadrangle(order, 4); // you provide the dof numbers after rotation // if you are using nodal elements, there are useful methods in class MeshNumbering Matrix<int> NumNodes2D(2, 2); NumNodes2D(0, 0) = 0; NumNodes2D(1, 0) = 1; NumNodes2D(1, 1) = 2; NumNodes2D(0, 1) = 3; Matrix<int> num; MeshNumbering<Dimension3>::GetRotationQuadrilateralFace(NumNodes2D, num); // you provide this array to nmap nmap.SetFacesDofRotationQuad(order, num);
Location :
SetSignDofRotationTri
Syntax
| void SetSignDofRotationTri(int order, const Matrix<bool>& is_negative) |
When you call this method you provide the change of signs after a rotation of a triangular face. If you want more details about the different orientations of a triangular face, you can look at the method GetRotationFaceDof.
Example :
int order = 4; NumberMap nmap; // 3 dofs inside the triangle nmap.SetNbDofTriangle(order, 3); // you provide the dof numbers after rotation // if you are using nodal elements, there are useful methods in class MeshNumbering VectR2 Points2D(3); Points2D(0) = R2(0.2, 0.2); Points2D(1) = R2(0.8, 0.2); Points2D(2) = R2(0.2, 0.8); Matrix<int> num; MeshNumbering<Dimension3>::GetRotationTriangularFace(Points2D, num); // you provide this array to nmap nmap.SetFacesDofRotationTri(order, num); // you can specify a change of signs // number of rows = 6 (6 different orientations for a triangle) // number of columns = 3 (here you specified 3 dofs on the triangle) Matrix<bool> sign(6, 3); // then you fill this matrix // basic example : only false (no change of signs) sign.Fill(false); nmap.SetSignDofRotationTri(order, sign);
Location :
SetSignDofRotationQuad
Syntax
| void SetSignDofRotationQuad(int order, const Matrix<bool>& is_negative) |
When you call this method you provide the change of signs after a rotation of a quadrilateral face. If you want more details about the different orientations of a triangular face, you can look at the method GetRotationFaceDof.
Example :
int order = 4; NumberMap nmap; // 4 dofs inside the quadrangle nmap.SetNbDofQuadrangle(order, 4); // you provide the dof numbers after rotation // if you are using nodal elements, there are useful methods in class MeshNumbering Matrix<int> NumNodes2D(2, 2); NumNodes2D(0, 0) = 0; NumNodes2D(1, 0) = 1; NumNodes2D(1, 1) = 2; NumNodes2D(0, 1) = 3; Matrix<int> num; MeshNumbering<Dimension3>::GetRotationQuadrilateralFace(NumNodes2D, num); // you provide this array to nmap nmap.SetFacesDofRotationQuad(order, num); // you can specify a change of signs // number of rows = 8 (8 different orientations for a square) // number of columns = 4 (here you specified 4 dofs on the quadrangle) Matrix<bool> sign(8, 4); // then you fill this matrix // basic example : only false (no change of signs) sign.Fill(false); nmap.SetSignDofRotationQuad(order, sign);
Location :
IsNegativeDof
Syntax
| bool IsNegativeDof(int rot, int order, int k, const Boundary& f) const |
This method returns true if the local dof k on the face f (edge in 2-D) with an orientation rot (compared to the global face) has a different sign than the global dof. The array containing the signs is given when you have called methods SetSignDofRotationTri and SetSignDofRotationQuad.
Example :
MeshNumbering<Dimension3> mesh_num(mesh);
// we assume that the mesh has been numbered correctly
// so that mesh.number_map is filled
// loop over elements
int order = mesh_num.GetOrder();
for (int i = 0; i < mesh.GetNbElt(); i++)
{
// loop over faces of this element
for (int j = 0; j < mesh.Element(i).GetNbFaces(); j++)
{
// we get orientation of the local face
int nf = mesh.Element(i).numFace(j);
int rot = mesh.Element(i).GetWayFace(j);
// loop over inside dofs of the face
int nb_dof = mesh_num.number_map.GetNbDofTriangle(order);
if (mesh_num.Boundary(nf).GetNbVertices() == 4)
nb_dof = mesh.number_map.GetNbDofQuadrangle(order);
for (int k = 0; k < nb_dof; k++)
cout << "Sign of dof " << k << " on face "
<< j << " and element " << i <<
" : " << mesh_num.number_map.IsNegativeDof(rot, order, k, mesh.Boundary(nf)) << endl;
}
}
Location :
GetRotationFaceDof
Syntax
| int GetRotationFaceDof(int rot, int order, int k, const Boundary& f) const |
This method returns the local dof number associated with a global dof, the orientation of the local face can be the same as the global face, or different. In the figure below, we have displayed the different orientations of triangular and quadrilateral face, 0, 1, 2, 3 are the vertex numbers of the global face. Orientation 0 corresponds to the case where the orientation is the same for the global and for the local face.
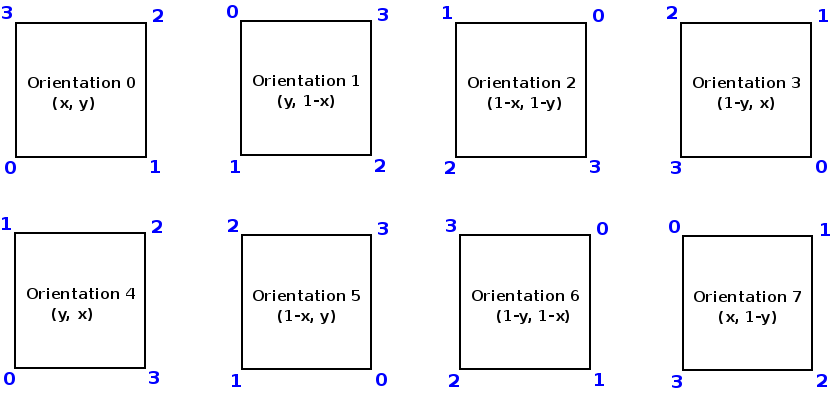
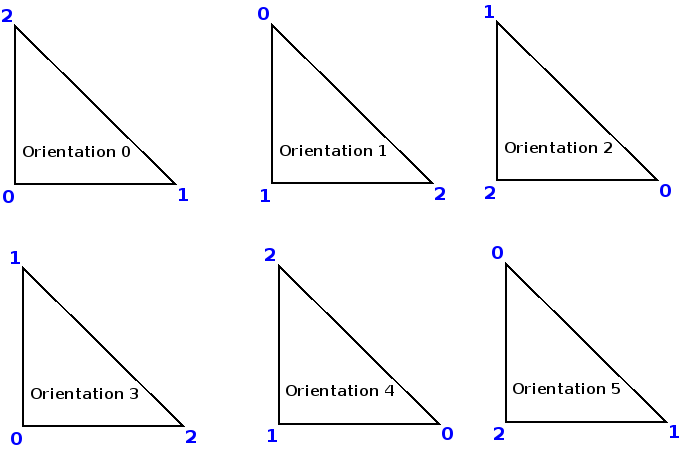
In the arguments, k is a dof on the global face (assumed to have an orientation equal to 0), rot is the orientation of the local face, and the method returns the corresponding dof number on the local face.
Example :
MeshNumbering<Dimension3> mesh_num(mesh);
// we assume that the mesh has been numbered correctly
// so that mesh.number_map is filled
// loop over elements
int order = mesh_num.GetOrder();
for (int i = 0; i < mesh.GetNbElt(); i++)
{
// loop over faces of this element
for (int j = 0; j < mesh.Element(i).GetNbFaces(); j++)
{
// we get orientation of the local face
int nf = mesh.Element(i).numFace(j);
int rot = mesh.Element(i).GetWayFace(j);
// loop over inside dofs of the face
int nb_dof = mesh_num.number_map.GetNbDofTriangle(order);
if (mesh.Boundary(nf).GetNbVertices() == 4)
nb_dof = mesh_num.number_map.GetNbDofQuadrangle(order);
for (int k = 0; k < nb_dof; k++)
cout << "Local dof number of dof " << k << " on face "
<< j << " and element " << i <<
" : " << mesh_num.number_map.GetRotationFaceDof(rot, order, k, mesh.Boundary(nf)) << endl;
}
}
Location :
Clear
Syntax
| void Clear() |
This method erases all the informations stored in the object.
Example :
NumberMap nmap; nmap.Clear();
Location :
Clear for ElementNumbering
Syntax
| void Clear() |
This method clears the dofs which have been constructed. The number of dofs associated with the face is equal to 0 after a call to that function. This low-level method should not be used, you can clear dof numbers of all the mesh by calling ClearDofs.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// and after you clear dofs
for (int i = 0; i < mesh.GetNbElt(); i++)
mesh_num.Element(i).Clear();
Location :
MeshElement.hxx
MeshElement.cxx
GetMemorySize for ElementNumbering
Syntax
| size_t GetMemorySize() const |
This method returns the memory used to store the object in bytes.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// and display the memory used to store dofs of element 0
cout << "Element 0 needs " << mesh_num.Element(0).GetMemorySize() << " bytes of storage";
Location :
MeshElement.hxx
MeshElement.cxx
GetNbDof for ElementNumbering
Syntax
| int GetNbDof() const |
This method returns the number of degrees of freedom associated with the element. Here we take into account intern degrees of freedom as well as degrees of freedom associated with the edges and vertices of the face. If the method NumberMesh has not been called, that will probably return 0.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// and display the number of degrees of freedom for an element
cout << "Element 0 contains " << mesh_num.Element(0).GetNbDof() << " degrees of freedom";
Location :
MeshElement.hxx
MeshElement.cxx
GetNumberDof for ElementNumbering
Syntax
| int GetNumberDof(int num_loc) const |
This method returns the global dof number of a local dof associated with the face. If the method NumberMesh has not been called, that won't work.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// you consider a global vector containing all the dofs of the mesh
VectReal_wp xsol(mesh_num.GetNbDof()); xsol.FillRand();
// then on each element, you retrieve the solution on local degrees of
// freedom, of course this doesn't work for every finite element
// since you don't take into account signs of dofs or linear combinations
for (int i = 0; i < mesh.GetNbElt(); i++)
{
VectReal_wp Uloc(mesh_num.Element(i).GetNbDof());
for (int j = 0; j < Uloc.GetM(); j++)
Uloc(j) = xsol(mesh_num.Element(i).GetNumberDof(j));
}
Location :
MeshElement.hxx
MeshElement.cxx
GetNodle for ElementNumbering
Syntax
| const IVect& GetNodle() const |
This method returns a reference to the array containing the dof numbers.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// you consider a global vector containing all the dofs of the mesh
VectReal_wp xsol(mesh_num.GetNbDof()); xsol.FillRand();
// then on each element, you retrieve the solution on local degrees of
// freedom, of course this doesn't work for every finite element
// since you don't take into account signs of dofs or linear combinations
for (int i = 0; i < mesh.GetNbElt(); i++)
{
VectReal_wp Uloc(mesh_num.Element(i).GetNbDof());
// you can make an alias, to have a shorter writing
const IVect& Nodle = mesh_num.Element(i).GetNodle();
for (int j = 0; j < Uloc.GetM(); j++)
Uloc(j) = xsol(Nodle(j));
}
Location :
MeshElement.hxx
MeshElement.cxx
GetNegativeDofNumber for ElementNumbering
Syntax
| const IVect& GetNegativeDofNumber() const |
This method returns a reference to the array containing local dofs for which the sign of local dof is opposite with the sign of global dof. This case occurs for edge elements, and hp finite elements.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// you consider a global vector containing all the dofs of the mesh
VectReal_wp xsol(mesh_num.GetNbDof()); xsol.FillRand();
// then on each element, you retrieve the solution on local degrees of
// freedom, of course this doesn't work for every finite element
// since you don't take into account signs of dofs or linear combinations
for (int i = 0; i < mesh.GetNbElt(); i++)
{
VectReal_wp Uloc(mesh_num.Element(i).GetNbDof());
// you can make an alias, to have a shorter writing
const IVect& Nodle = mesh_num.Element(i).GetNodle();
for (int j = 0; j < Uloc.GetM(); j++)
Uloc(j) = xsol(Nodle(j));
// you retrieve dofs with opposite sign, and change the sign, to
// get the correct vector
const IVect& neg = mesh_num.Element(i).GetNegativeDofNumber();
for (int j = 0; j < neg.GetM(); j++)
Uloc(neg(j)) = -Uloc(neg(j));
}
Location :
MeshElement.hxx
MeshElement.cxx
SetNegativeDofNumber for ElementNumbering
Syntax
| void SetNegativeDofNumber(const IVect& num) |
By calling this method, you provide the dof numbers for which the sign of local dofs is opposite to the sign of global dofs. Currently, this method is only used when you call NumberMesh, so you shouldn't call directly this method.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
// you number mesh (we assume that number_map has been modified)
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// you consider a global vector containing all the dofs of the mesh
VectReal_wp xsol(mesh_num.GetNbDof()); xsol.FillRand();
// then on each element, you retrieve the solution on local degrees of
// freedom, of course this doesn't work for every finite element
// since you don't take into account signs of dofs or linear combinations
for (int i = 0; i < mesh.GetNbElt(); i++)
{
// you can sort dofs for which negative sign has to be applied
IVect neg = mesh_num.Element(i).GetNegativeDofNumber();
Sort(neg);
mesh_num.Element(i).SetNegativeDofNumber(neg);
}
Location :
MeshElement.hxx
MeshElement.cxx
ReallocateDof for ElementNumbering
Syntax
| void ReallocateDof(int nb_dof) |
This method lets you change the number of degrees of freedom associated with the face. Previous dof numbers will be lost, if you want to keep them, it is better to use AddDof. In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// on each element, you decide a given number of degrees of freedom
for (int i = 0; i < mesh.GetNbElt(); i++)
{
mesh_num.Element(i).ReallocateDof(5);
// of course, you have to provide the global dofs
for (int j = 0; j < 5; j++)
mesh_num.Element(i).SetNumberDof(j, i*5+j);
}
Location :
MeshElement.hxx
MeshElement.cxx
SetNumberDof for ElementNumbering
Syntax
| void SetNumberDof(int num_loc, int num_glob) |
With this method, you can specify the global number of a local degree of freedom on the face. In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// on each element, you decide a given number of degrees of freedom
for (int i = 0; i < mesh.GetNbElt(); i++)
{
mesh_num.Element(i).ReallocateDof(5);
// of course, you have to provide the global dofs
for (int j = 0; j < 5; j++)
mesh_num.Element(i).SetNumberDof(j, i*5+j);
}
Location :
MeshElement.hxx
MeshElement.cxx
AddDof for ElementNumbering
Syntax
| void AddDof(int nb_new_dof) |
With this method, you can increase the number of degrees of freedom on a face, while keeping previous dof numbers. You provide the number of degrees of freedom you wish to add. In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// on each element, you decide a given number of degrees of freedom
for (int i = 0; i < mesh.GetNbElt(); i++)
{
mesh_num.Element(i).ReallocateDof(5);
// of course, you have to provide the global dofs
for (int j = 0; j < 5; j++)
mesh_num.Element(i).SetNumberDof(j, i*5+j);
// we add two degrees of freedom
mesh_num.Element(i).AddDof(2);
// then you have to provide dof numbers of these new dofs
for (int j = 0; j < 2; j++)
mesh_num.Element(i).SetNumberDof(5+j, 5*mesh.GetNbElt()+2*i+j);
}
Location :
MeshElement.hxx
MeshElement.cxx
PushDof for ElementNumbering
Syntax
| void PushDof(int dof_num) |
When you have only one degree of freedom to add, instead of calling AddDof(1) and SetNumberDof, you can directly call this method. The provided number will be added at the end of the array containing the dof numbers. In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// on each element, you decide a given number of degrees of freedom
for (int i = 0; i < mesh.GetNbElt(); i++)
{
mesh_num.Element(i).ReallocateDof(5);
// of course, you have to provide after the global dofs
for (int j = 0; j < 5; j++)
mesh_num.Element(i).SetNumberDof(j, i*5+j);
// we add a degree of freedom
mesh_num.Element(i).PushDof(mesh.GetNbElt()+i);
}
Location :
MeshElement.hxx
MeshElement.cxx
ReallocateFaces for ElementNumbering
Syntax
| void ReallocateFaces(int nb_faces) |
This method informs how many faces the element should contain. In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// you allocate the number of faces
mesh_num.Element(0).ReallocateFaces(3);
// and provide the order of integration for each face and offset
mesh_num.Element(0).SetOrderFace(0, 2, 0);
mesh_num.Element(0).SetOrderFace(1, 3, 9);
mesh_num.Element(0).SetOrderFace(2, 4, 25);
Location :
MeshElement.hxx
MeshElement.cxx
SetOrderFace for ElementNumbering
Syntax
| void SetOrderFace(int num_loc, int order, int offset) |
This method informs for the local face num_loc, the used order of integration and offset (for integration points). In regular use, you should not call this method since it is already called in NumberMesh.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
// you allocate the number of faces
mesh_num.Element(0).ReallocateFaces(3);
// and provide the order of integration for each face and offset
mesh_num.Element(0).SetOrderFace(0, 2, 0);
mesh_num.Element(0).SetOrderFace(1, 3, 9);
mesh_num.Element(0).SetOrderFace(2, 4, 25);
Location :
MeshElement.hxx
MeshElement.cxx
GetOrderFace for ElementNumbering
Syntax
| int GetOrderFace(int num_loc) const |
This method returns the order of integration associated with the face num_loc of the element.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// order of integration of face 1 of element 0
int r = mesh_num.Element(0).GetOrderFace(1);
Location :
MeshElement.hxx
MeshElement.cxx
GetOffsetFace for ElementNumbering
Syntax
| int GetOffsetFace(int num_loc) const |
This method returns the offset used for integration points associated with the face num_loc of the element.
Example :
Mesh<Dimension2> mesh;
// we read a mesh
mesh.Read("test.mesh");
MeshNumbering<Dimension2> mesh_num(mesh);
mesh_num.NumberMesh();
// order of integration of face 1 of element 0
int r = mesh_num.Element(0).GetOrderFace(1);
// offset to access integration points of this face
// integration points of face 0 will be between 0 and n1
// integration points of face 1 will be between n1 and n2
// integration points of face 2 will be between n2 and n3
// ...
// the offset is the integer 0, n1, n2 (for faces 0, 1 and 2)
int offset = mesh_num.Element(0).GetOffsetFace(1);
Location :
MeshElement.hxx
MeshElement.cxx
GetMemorySize for NumberMap
Syntax
| size_t GetMemorySize() const |
This method returns the memory used to store the object in bytes.
Example :
NumberMap nmap; // and display the memory used to store the object cout << "nmap needs " << nmap.GetMemorySize() << " bytes of storage";
Location :
GetDofNumberOnElement for NumberMap
Syntax
| IVect GetDofNumberOnElement(const MeshNumbering& mesh_num, int i ) const |
This method returns the dof numbers of the element i.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); // assuming that mesh_num will be numbered // we want to retrieve the numbers of the degrees of freedom on an element int num_elem = 42; IVect Nodle = mesh_num.number_map.GetDofNumberOnElement(num_elem); // and display these numbers cout << "dof numbers = " << Nodle << endl;
Location :
GetLocalUnknownVector for NumberMap
Syntax
| void GetLocalUnknownVector(const MeshNumbering& mesh_num, const Vector& E, int i, Vector<Vector>& Eloc ) const |
This method returns extracts the values of E on the degrees of freedom of the element i. The resulting vector Eloc is a vector of vector because there can be several unknowns in the input vector E. On input the vector Eloc must be allocated with the number of unknowns. If there are only invariant dofs by rotation, this operation is equivalent to Eloc = E(num_dof) where num_dof are the numbers of the degrees of freedom on the element i.
Parameters
- mesh_num (in)
- mesh numbering
- E (in)
- vector to treat
- i (in)
- element number
- Eloc (inout)
- values of E on degrees on freedom of element i
Example :
// we construct a numbering
MeshNumbering<Dimension2> mesh_num(mesh);
int order = 3;
mesh_num.SetOrder(order);
mesh_num.number_map.SetOrder(mesh, order);
// E is a vector containing several unknowns
enum{nb_unknowns = 3; }
int Ndof = mesh_num.GetNbDof();
// E(m*Ndof + i) is the i-th component of E_m (m : unknown number)
VectReal_wp E(nb_unknowns*Ndof); E.FillRand();
// then you can extract values on a single element of the mesh
int num_elem = 42;
Vector<VectReal_wp> Eloc(nb_unknowns);
mesh_num.number_map.GetLocalUnknownVector(mesh_num, E, num_elem, Eloc);
// you can also use TinyVector
TinyVector<VectReal_wp, nb_unknowns> E_loc;
mesh_num.number_map.GetLocalUnknownVector(mesh_num, E, num_elem, E_loc);
Location :
AddLocalUnknownVector for NumberMap
Syntax
| void AddLocalUnknownVector(const MeshNumbering& mesh_num, T alpha, TinyVector<Vector, m>& Eloc, int i, Vector<Vector>& E ) const |
This method adds the local values of Eloc to the global vector E. If there are only invariant dofs by rotation, this operation is equivalent to E(num_dof) = E(num_dof) + alpha*Eloc where num_dof are the numbers of the degrees of freedom on the element i.
Parameters
- mesh_num (in)
- mesh numbering
- alpha (in)
- coefficient (real or complex)
- Eloc (inout)
- local values to add (may be modified)
- i (in)
- element number
- E (inout)
- global vector
Example :
// we construct a numbering
MeshNumbering<Dimension2> mesh_num(mesh);
int order = 3;
mesh_num.SetOrder(order);
mesh_num.number_map.SetOrder(mesh, order);
// E is a vector containing several unknowns
enum{ nb_unknowns = 3};
int Ndof = mesh_num.GetNbDof();
// E(m*Ndof + i) is the i-th component of E_m (m : unknown number)
VectReal_wp E(nb_unknowns*Ndof); E.FillRand();
// contribution on a given element
int num_elem = 42;
int nb_local = mesh_num.GetNbLocalDof(num_elem);
TinyVector<VectReal_wp, 3> Eloc;
Eloc(0).Reallocate(nb_local); Eloc(0).FillRand();
Eloc(1).Reallocate(nb_local); Eloc(1).FillRand();
Eloc(2).Reallocate(nb_local); Eloc(2).FillRand();
// we add these local contributions (multiplied by alpha) to the global vector
Real_wp alpha = 2.0;
mesh_num.number_map.AddLocalUnknownVector(mesh_num, alpha, Eloc, num_elem, E);
Location :
ModifyLocalComponentVector for NumberMap
Syntax
| void ModifyLocalComponentVector(const MeshNumbering& mesh_num, const Vector& U, int i) const |
This method modifies the vector U such that values on global degrees of freedom are transformed into values on local degrees on freedom. If the degrees of freedom are invariant by rotation, the method does not change the vector U. The local basis functions can be expressed with a linear combination of global basis functions:
φloci = Σ Ai, j φglobj
where the matrix A only depends on the difference of orientation between local edges (and faces) and global edges (and faces). The method ModifyLocalComponentVector applies this operator A to the vector U. When you call GetLocalUnknownVector the values are extracted and then multiplied by this operator in order to have values on local degrees of freedom.
Parameters
- mesh_num (in)
- mesh numbering
- U (inout)
- vector to modify
- i (in)
- element number
Example :
// we construct a numbering MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; mesh_num.SetOrder(order); mesh_num.number_map.SetOrder(mesh, order); // E is a vector containing values on all degrees of freedom int Ndof = mesh_num.GetNbDof(); VectReal_wp E(Ndof); E.FillRand(); // you can extract values for dofs of an element int num_elem = 42; int nb_loc = mesh_num.GetNbLocalDof(num_elem); VectReal_wp Eloc(nb_loc); IVect num_dof = number_map.GetDofNumberOnElement(mesh_num.Element(num_elem), num_elem); for (int i = 0; i < nb_loc; i++) Eloc(i) = E(num_dof(i)); // then you apply the operator A, to obtain values on local degrees of freedom mesh_num.number_map.ModifyLocalComponentVector(mesh_num, Eloc, num_elem); // these two operations (extraction + application) are equivalent to GetLocalUnknownVector
Related topics :
GetLocalUnknownVectorLocation :
ModifyLocalUnknownVector for NumberMap
Syntax
| void ModifyLocalUnknownVector(const MeshNumbering& mesh_num, const Vector& U, int i) const |
This method modifies the vector U such that the transpose operator A is applied to vector U. If the degrees of freedom are invariant by rotation, the method does not change the vector U. The local basis functions can be expressed with a linear combination of global basis functions:
φloci = Σ Ai, j φglobj
where the matrix A only depends on the difference of orientation between local edges (and faces) and global edges (and faces). The method ModifyLocalComponentVector applies this operator A to the vector U. The method ModifyLocalUnknownVector applies the transpose operator A, this operator is usually implied when you integrate against global basis functions (or their gradients). When you call AddLocalUnknownVector the values are multiplied by this transpose operator and added to the global vector.
Parameters
- mesh_num (in)
- mesh numbering
- U (inout)
- vector to modify
- i (in)
- element number
Example :
// we construct a numbering MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; mesh_num.SetOrder(order); mesh_num.number_map.SetOrder(mesh, order); // E is a vector containing values on all degrees of freedom int Ndof = mesh_num.GetNbDof(); VectReal_wp E(Ndof); E.FillRand(); // we want to add local terms coming from integrals against basis functions on E int num_elem = 42; int nb_loc = mesh_num.GetNbLocalDof(num_elem); VectReal_wp Eloc(nb_loc); IVect num_dof = number_map.GetDofNumberOnElement(mesh_num.Element(num_elem), num_elem); Eloc.FillRand(); // you apply the transpose operator A mesh_num.number_map.ModifyLocalUnknownVector(mesh_num, Eloc, num_elem); // then add the values to the vector E for (int i = 0; i < nb_loc; i++) E(num_dof(i)) += Eloc(i); // these two operations (application + addition) are equivalent to AddLocalUnknownVector
Related topics :
AddLocalUnknownVectorLocation :
GetGlobalUnknownVector for NumberMap
Syntax
| void GetGlobalUnknownVector(const MeshNumbering& mesh_num, const Vector<Vector>& U, int i) const |
This method computes the components of a vector in global degrees of freedom from its components on local dofs. It modifies the vectors U(m) (m : unknown number) such that the operator A-1 is applied to vector U. If the degrees of freedom are invariant by rotation, the method does not change the vector U. The local basis functions can be expressed with a linear combination of global basis functions:
φloci = Σ Ai, j φglobj
where the matrix A only depends on the difference of orientation between local edges (and faces) and global edges (and faces). The method ModifyLocalComponentVector applies this operator A to the vectors U(m). The method GetGlobalUnknownVector applies the operator A-1 to the vectors U(m). These two methods are reciprocal from each other.
Parameters
- mesh_num (in)
- mesh numbering
- U (inout)
- vector to modify
- i (in)
- element number
Example :
// we construct a numbering MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; mesh_num.SetOrder(order); mesh_num.number_map.SetOrder(mesh, order); // numbers of dofs on a given element int num_elem = 42; int nb_loc = mesh_num.GetNbLocalDof(num_elem); Vector<VectReal_wp> Eloc(1); Eloc(0).Reallocate(nb_loc); IVect num_dof = number_map.GetDofNumberOnElement(mesh_num.Element(num_elem), num_elem); // we compute a vector with local dofs : Eloc(0).FillRand(); // we want to project it on global dofs mesh_num.number_map.GetGlobalUnknownVector(mesh_num, Eloc, num_elem); // then copy the obtained values on a global vector VectReal_wp E(mesh_num.GetNbDof()); for (int i = 0; i < nb_loc; i++) E(num_dof(i)) = Eloc(i);
Related topics :
ModifyLocalComponentVectorLocation :
ModifyLocalRowMatrix for NumberMap
Syntax
| void ModifyLocalRowMatrix(const MeshNumbering& mesh_num, const Matrix& A, int i, int nb_u) const |
This method modifies rows of the matrix to transform a matrix with rows associated with local dofs to a matrix with rows associated with global dofs. When local finite element matrices are computed, you have to call ModifyLocalRowMatrix and ModifyLocalColumnMatrix to obtain a matrix that can be added to the global finite element matrix. If the last argument nb_u is not provided, the number of unknowns is computed from the number of rows of the given matrix. If degrees of freedom are invariant by rotation, the matrix will be unchanged.
Parameters
- mesh_num (in)
- mesh numbering
- A (inout)
- matrix to modify
- i (in)
- element number
- nb_u (optional)
- number of unknowns
Example :
// we construct a numbering
MeshNumbering<Dimension2> mesh_num(mesh);
int order = 3;
mesh_num.SetOrder(order);
mesh_num.number_map.SetOrder(mesh, order);
// numbers of dofs on a given element
int num_elem = 42;
int nb_loc = mesh_num.GetNbLocalDof(num_elem);
Vector<VectReal_wp> Eloc(1); Eloc(0).Reallocate(nb_loc);
IVect num_dof = number_map.GetDofNumberOnElement(mesh_num.Element(num_elem), num_elem);
// we compute a local finite element matrix
Matrix<Real_wp> Aloc(nb_loc, nb_loc);
Aloc.FillRand();
// projection to global dofs
mesh_num.number_map.ModifyLocalRowMatrix(mesh_num, Aloc, num_elem, 1);
mesh_num.number_map.ModifyLocalColumnMatrix(mesh_num, Aloc, num_elem, 1);
// then add the matrix to a global one
Matrix<Real_wp, General, ArrayRowSparse> A;
for (int i = 0; i < nb_loc; i++)
for (int j = 0; j < nb_loc; j++)
A.AddInteraction(num_dof(i), num_dof(j), Aloc(i, j));
Location :
ModifyLocalColumnMatrix for NumberMap
Syntax
| void ModifyLocalColumnMatrix(const MeshNumbering& mesh_num, const Matrix& A, int i, int nb_u) const |
This method modifies column of the matrix to transform a matrix with columns associated with local dofs to a matrix with columns associated with global dofs. When local finite element matrices are computed, you have to call ModifyLocalRowMatrix and ModifyLocalColumnMatrix to obtain a matrix that can be added to the global finite element matrix. If the last argument nb_u is not provided, the number of unknowns is computed from the number of columns of the given matrix. If degrees of freedom are invariant by rotation, the matrix will be unchanged.
Parameters
- mesh_num (in)
- mesh numbering
- A (inout)
- matrix to modify
- i (in)
- element number
- nb_u (optional)
- number of unknowns
Example :
// we construct a numbering
MeshNumbering<Dimension2> mesh_num(mesh);
int order = 3;
mesh_num.SetOrder(order);
mesh_num.number_map.SetOrder(mesh, order);
// numbers of dofs on a given element
int num_elem = 42;
int nb_loc = mesh_num.GetNbLocalDof(num_elem);
Vector<VectReal_wp> Eloc(1); Eloc(0).Reallocate(nb_loc);
IVect num_dof = number_map.GetDofNumberOnElement(mesh_num.Element(num_elem), num_elem);
// we compute a local finite element matrix
Matrix<Real_wp> Aloc(nb_loc, nb_loc);
Aloc.FillRand();
// projection to global dofs
mesh_num.number_map.ModifyLocalRowMatrix(mesh_num, Aloc, num_elem, 1);
mesh_num.number_map.ModifyLocalColumnMatrix(mesh_num, Aloc, num_elem, 1);
// then add the matrix to a global one
Matrix<Real_wp, General, ArrayRowSparse> A;
for (int i = 0; i < nb_loc; i++)
for (int j = 0; j < nb_loc; j++)
A.AddInteraction(num_dof(i), num_dof(j), Aloc(i, j));
Location :
GetNbPointsQuadBoundary
Syntax
| int GetNbPointsQuadBoundary(int order, const Boundary& f) const |
This method returns the number of quadrature points for a given face.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on a face int num_face = 41; cout << "Number of quadrature points " << mesh_num.number_map.GetNbPointsQuadBoundary(order, mesh.Boundary(num_face));
Location :
GetQuadraturePoint
Syntax
| Real_wp GetQuadraturePoint(int order, int k, const Edge<Dimension2>& f) const |
| R2 GetQuadraturePoint(int order, int k, const Face<Dimension3>& f) const |
This method returns the k-th quadrature point of a face (or edge in 2-D) of a mesh.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on a face int num_face = 41; cout << "Number of quadrature points " << nmap.GetNbPointsQuadBoundary(order, mesh.Boundary(num_face)); // and quadrature points cout << "First Quadrature point = " << nmap.GetQuadraturePoint(order, 0, mesh.Boundary(num_face)) << endl;
Location :
ConstructQuadrature2D
Syntax
| void ConstructQuadrature2D(const TinyVector<IVect, 4>& order, int type_quad = 0) |
This method constructs quadrature points on the unit interval [0, 1] for the given orders. These quadrature points can then be used for the boundary integrals of 2-D meshes. The last argument is optional and is the type of quadrature rule (as proposed in class Globatto).
Example :
NumberMap nmap; TinyVector<IVect, 4> order; // in 2-D only order(0) is used order(0).Reallocate(3); order(0)(0) = 1; order(0)(1) = 4; order(0)(2) = 5; // orders needed nmap.ConstructQuadrature2D(order); // points can be retrieved with GetEdgeQuadrature const VectReal_wp& pts = nmap.GetEdgeQuadrature(4);
Location :
ConstructQuadrature3D
Syntax
| void ConstructQuadrature3D(const TinyVector<IVect, 4>& order, int type_tri = 0, int type_quad = 0) |
This method constructs quadrature points on the unit triangle for orders given in order(0), and on the unit square for orders given in order(1). These quadrature points can then be used for the boundary integrals of 3-D meshes. The last arguments are optional and are the type of quadrature rule for triangles and quadrilaterals.
Example :
NumberMap nmap; TinyVector<IVect, 4> order; // in 3-D only order(0) and order(1) are used order(0).Reallocate(3); order(0)(0) = 1; order(0)(1) = 4; order(0)(2) = 5; // orders needed for triangles order(1).Reallocate(4); order(1)(0) = 1; order(1)(1) = 2; order(1)(2) = 4; order(1)(3) = 5; // orders needed for quadrangles nmap.ConstructQuadrature3D(order); // points can be retrieved with GetTriangleQuadrature / GetQuadrangleQuadrature const VectR2& pts_tri = nmap.GetTriangleQuadrature(4); const VectR2& pts_quad = nmap.GetQuadrangleQuadrature(4);
Location :
GetEdgeQuadrature
Syntax
| const VectReal_wp& GetEdgeQuadrature(int order) const |
This method returns the integration points for the unit interval at the given order.
Example :
MeshNumbering<Dimension2> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element TriangleClassical tri; tri.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tri.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on an edge int num_edge = 41; cout << "Number of quadrature points " << nmap.GetNbPointsQuadBoundary(order, mesh.Boundary(num_edge)); // and quadrature points const VectReal_wp& pts = nmap.GetEdgeQuadrature(order);
Location :
GetTriangleQuadrature
Syntax
| const VectR2& GetTriangleQuadrature(int order) const |
This method returns the integration points for the unit triangle at the given order.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on a face int num_face = 41; cout << "Number of quadrature points " << nmap.GetNbPointsQuadBoundary(order, mesh.Boundary(num_face)); // and quadrature points const VectR2& pts = nmap.GetTriangleQuadrature(order);
Location :
GetQuadrangleQuadrature
Syntax
| const VectR2& GetQuadrangleQuadrature(int order) const |
This method returns the integration points for the unit square at the given order.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element HexahedronLobatto hex; hex.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; hex.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on a face int num_face = 41; cout << "Number of quadrature points " << nmap.GetNbPointsQuadBoundary(order, mesh.Boundary(num_face)); // and quadrature points const VectR2& pts = nmap.GetQuadrangleQuadrature(order);
Location :
SetPointsQuadratureQuadrangle
Syntax
| void SetPointsQuadratureQuadrangle(int order, const VectR2& points) |
This method sets the integration points for the unit square at the given order.
Example :
NumberMap nmap; int order = 3; VectR2 pts; VectReal_wp weights; QuadrangleQuadrature::ConstructQuadrature(2*order, pts, weights); nmap.SetPointsQuadratureQuadrangle(order, pts);
Location :
SetPointsQuadratureTriangle
Syntax
| void SetPointsQuadratureTriangle(int order, const VectR2& points) |
This method sets the integration points for the unit triangle at the given order.
Example :
NumberMap nmap; int order = 3; VectR2 pts; VectReal_wp weights; TriangleQuadrature::ConstructQuadrature(2*order, pts, weights); nmap.SetPointsQuadratureTriangle(order, pts);
Location :
SetPointsQuadratureEdge
Syntax
| void SetPointsQuadratureEdge(int order, const VectReal_wp& points) |
This method sets the integration points for the unit interval at the given order.
Example :
NumberMap nmap; int order = 3; VectReal_wp pts; VectReal_wp weights; ComputeGaussLegendre(pts, weights, order); nmap.SetPointsQuadratureEdge(order, pts);
Location :
SetFluxWeightEdge
Syntax
| void SetFluxWeightEdge(int order, const VectReal_wp& weight) |
This method sets the integration weights (divided by two) for the unit interval at the given order.
Example :
NumberMap nmap; int order = 3; VectReal_wp pts; VectReal_wp weights; ComputeGaussLegendre(pts, weights, order); nmap.SetPointsQuadratureEdge(order, pts); weights *= 0.5; nmap.SetFluxWeightEdge(order, weights);
Location :
SetFluxWeightTriangle
Syntax
| void SetFluxWeightTriangle(int order, const VectReal_wp& weight) |
This method sets the integration weights (divided by two) for the unit triangle at the given order.
Example :
NumberMap nmap; int order = 3; VectR2 pts; VectReal_wp weights; TriangleQuadrature::ConstructQuadrature(2*order, pts, weights); nmap.SetPointsQuadratureTriangle(order, pts); weights *= 0.5; nmap.SetFluxWeightTriangle(order, weights);
Location :
SetFluxWeightQuadrangle
Syntax
| void SetFluxWeightQuadrangle(int order, const VectReal_wp& weight) |
This method sets the integration weights (divided by two) for the unit square at the given order.
Example :
NumberMap nmap; int order = 3; VectR2 pts; VectReal_wp weights; QuadrangleQuadrature::ConstructQuadrature(2*order, pts, weights); nmap.SetPointsQuadratureQuadrangle(order, pts); weights *= 0.5; nmap.SetFluxWeightQuadrangle(order, weights);
Location :
GetFluxWeight
Syntax
| const VectReal_wp& GetFluxWeight(int order, const Edge<Dimension2>& f) const |
| const VectReal_wp& GetFluxWeight(int order, const Face<Dimension3>& f) const |
This method returns the integration weights (divided by two) of a face (or edge in 2-D) of a mesh.
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // you can display number of quadrature points on a face int num_face = 41; cout << "Number of quadrature points " << nmap.GetNbPointsQuadBoundary(order, mesh.Boundary(num_face)); // and quadrature points cout << "First Quadrature point = " << nmap.GetQuadraturePoint(order, 0, mesh.Boundary(num_face)) << endl; // and weights divided by two const VectReal_wp& half_weights = nmap.GetFluxWeight(order);
Location :
GetRotationQuadraturePoints
Syntax
| const Matrix<int>& GetRotationQuadraturePoints(int order, const Edge<Dimension2>& f) const |
| const Matrix<int>& GetRotationQuadraturePoints(int order, const Face<Dimension3>& f) const |
This method returns the new numbers of quadrature points after a rotation of a face (edge in 2-D). These numbers are stored in a matrix, each row is associated with a different rotation. These numbers are automatically computed as soon as you provided quadrature points (with methods such as SetPointsQuadratureTriangle, ConstructQuadrature3D, etc).
Example :
MeshNumbering<Dimension3> mesh_num(mesh); int order = 3; NumberMap& nmap = mesh_num.number_map; // we construct a finite element TetrahedronClassical tet; tet.ConstructFiniteElement(order); // then number_map int dg_form = ElementReference_Base::CONTINUOUS; tet.ConstructNumberMap(mesh_num.number_map, dg_form); // numbers of quadrature points after rotation/symmetry of a face int num_face = 41; const Matrix<int>& RotQuad = mesh_num.number_map.GetRotationQuadraturePoints(order, mesh.Boundary(num_face)); // RotQuad(1, :) are the new numbers for the first rotation // RotQuad(2, :) are the new numbers for the second rotation // etc
Location :
GetGmshTriangularNumbering
Syntax
| static void GetGmshTriangularNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of a triangle with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshTriangularNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshQuadrilateralNumbering
Syntax
| static void GetGmshQuadrilateralNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of a quadrangle with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshQuadrilateralNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshTetrahedralNumbering
Syntax
| static void GetGmshTetrahedralNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of a tetrahedron with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshTetrahedralNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshPyramidalNumbering
Syntax
| static void GetGmshPyramidalNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of a pyramid with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshPyramidalNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshPrismaticNumbering
Syntax
| static void GetGmshPrismaticNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of a triangular prism with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshPrismaticNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshHexahedralNumbering
Syntax
| static void GetGmshHexahedralNumbering(int order, IVect& num) |
This method fills the array num that links Gmsh numbering of an hexahedron with Montjoie numbering. Indeed num(i) is the Montjoie number of the Gmsh dof i.
Example :
IVect num; int order = 3; NumberMap::GetGmshHexahedralNumbering(order, num); // num(dof_gmsh) = dof_montjoie
Location :
GetGmshEntityNumber
Syntax
| static int GetGmshEntityNumber(const Edge& elt, int order) |
| static int GetGmshEntityNumber(const Face& elt, int order) |
| static int GetGmshEntityNumber(const Volume& elt, int order) |
This method returns the entity number (as needed in .msh format) of an element of the mesh.
Example :
Mesh<Dimension3> mesh;
mesh.Read("test.mesh");
int order = 3;
int num = NumberMap::GetGmshEntityNumber(mesh.Boundary(2), order);
num = NumberMap::GetGmshEntityNumber(mesh.Element(3), order);