Simulation d'un processus AR(p)

1. Simuler un processus bruit blanc $N(0,0.2^2)$, avec 500 instants.

   Corrigé

    
   title1 'Simulated Bruit Blanc Gaussien N(0,0.2^2) Series';
     data bbg;
      do i = 1 to 500;
          a = 0.2*rannor( 32565 );
          output;
      end;
     run;
     symbol1 interpol=join color=black value=none;
   proc gplot data=bbg;
      plot a*i;
   run;
   

2. Si on veut obtenir un trajectoire different, comme faire ?

   Corrigé Il suffit de changer le nombre 32565

3. Simuler un processus AR(1) : $X_{t} = 0.75X_{t-1}+\varepsilon _t$ avec $\varepsilon _t\sim N(0,0.2^2)$.

   Corrigé

    
   title1 'Simulated AR(1)';
   data a;
       u1 = 0;
       do i = -50 to 500;
          a = rannor( 32565 );
          u = 0.75*u1 + 0.2*a;
          if i > 0 then output;         
          u1 = u;
       end;
     run;
     symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   

4. Changer le coeffficient 0.75 à 1.

   Corrigé C'est un marche aléatoire, processus non stationnaire.

5. Changer le coeffficient 0.75 à 1.1, que constatez vous ?

   Corrigé le processus n'est pas stationnaire.

6. Simuler un processus AR(2) : $$X_{t} -\phi_1 X_{t-1} -\phi_2 X_{t-2} = \varepsilon _t$$, avec $\phi_1=\frac56$ et $\phi_2=-\frac16$.

   Corrigé

    
   
   title1 'Simulated AR(2)';
   data a;
       u1 = 0; u2=0;
       do i = -50 to 500;
          a = rannor( 32565 );
          u = (5.0/6)*u1 -(1.0/6)*u2 + 0.2*a;
          if i > 0 then output;         
          u2 = u1; u1 = u;         
       end;
     run;
   
   symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   

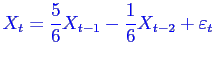7. Remarquer la difference entre le processus $$X_{t} = \frac56 X_{t-1} -\frac16 X_{t-2} + \varepsilon _t$$ et le processus 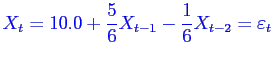$$X_{t} = 10.0 + \frac56 X_{t-1} -\frac16 X_{t-2} = \varepsilon _t$$ (simuler le). Quelles sont les moyennes théoriques de ces processus ?

   Corrigé la moyenne du premier proc est 0, la moyenne de la seconde est $\frac{10}{1-\phi_1-\phi_2} = 30.0$. (vérifier graphiquement).