Simulation d'un processus MA(q) et ARIMA(p,d,q)

1. Simuler le processus suivant
   
   $$X_t = (1-2.4B+0.8B^2)\varepsilon _t  \mbox{o\\lq u}   \varepsilon \sim N(0,0.2^2)$$
   
   

   Corrigé

    
   title1 'Simulated MA(2)';
   data a;
       a1 = 0; a2=0;
       do i = -50 to 500;
          a = 0.2*rannor( 32565 );
          u = a - 2.4*a1 + 0.8*a2;
          if i > 0 then output;         
          a2 = a1; a1 = a;
       end;
     run;
   symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   

2. Simuler un processus tel que
   
   $$X_t-X_{t-1} = (1-2.4B+0.8B^2)\varepsilon _t   \mbox{o\\lq u}   \varepsilon \sim N(0,0.2^2)$$
   
   

   Corrigé

    
   title1 'Simulated ARIMA(0,1,2)';
   data a;
       u1=0; a1 = 0; a2=0;
       do i = -50 to 500;
          a = 0.2*rannor( 32565 );
          u = u1 + a - 2.4*a1 + 0.8*a2;
          if i > 0 then output;         
          u1 = u; a2 = a1; a1 = a;
       end;
     run;
     symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   

3. Soit $X_t$ un processus ARIMA(0,1,2) simulé par la méthode ci-dessus. Comment utiliser ce resultat pour simuler le processus $Y_t \stackrel{\triangle}{=}X_t-X_{t-1}$.

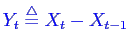   Corrigé Ajouter à la suite de la question précedente

    
   data a;
      set a;
      udif = dif(u);
   run;
   
   title1 "Transformed Series";
   proc gplot data=a;
      plot udif*i;
   run;
   quit;
   

   Normalement on obtient un processus stationnaire.

4. Simuler le processus ARIMA(2,1,2) suivant
   
   $$\bgroup\color{blue} \displaystyle (1-\frac56 B+ \frac16 B^... ...epsilon _t   \mbox{o\\lq u}   \varepsilon \sim N(0,0.2^2) \egroup$$
   
   
   Et calculer et tracer le processus $Y_t=(1-B)X_t$

   Corrigé Nous avons
   

   $$\bgroup\color{blue}(1-\frac56 B+ \frac16 B^2) (1-B) = 1-\frac{11}{6}B + B^2 -\frac16 B^3\egroup$$
   
   
   donc $X_t = \frac{11}{6}X_{t-1} - X_{t-2} +\frac16 X_{t-3}$

    
   title1 'Simulated ARIMA(2,1,2)';
   data a;
       u1=0; u2=0; u3=0.0; a1 = 0; a2=0;
       do i = -50 to 500;
          a = 0.2*rannor( 32565 );
          u = (11.0/6)*u1 - u2 + (1/6)*u3 + a - 2.4*a1 + 0.8*a2;
          if i > 0 then output;         
          u3 = u2; u2 = u1; u1 = u; a2 = a1; a1 = a;
       end;
     run;
   symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   
   data a;
      set a;
      udif = dif(u);
   run;
   
   title1 "Transformed Series";
   proc gplot data=a;
      plot udif*i;
   run;
   quit;
   

5. Modifier la condition initiale de $(X_{-1}, X_{-2}, X_{-3}, \varepsilon_{-1},\varepsilon _{-2})$. Etudier la sensibilité.