Exemples
On trouvera ici des exemples de groupes Kleiniens, ensembles limites, domaines fondamentaux (à ajouter : cœurs convexes).
On pourra également consulter la page web de McMullen qui contient de nombreuses images (peu sont commentées).
Sommaire
Exemple de Fricke et Klein
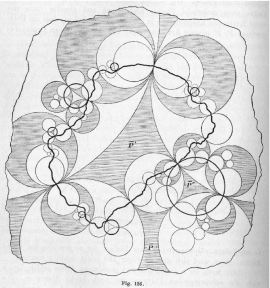
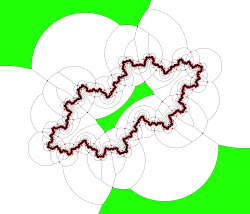
Le dessin ci-dessous illustre un livre de Fricke et Klein paru en 1897.
C'est un exemple de groupe de réflexion (qui contient un groupe Kleinien d'indice 2) sur 5 cercles tangents. Les tangences ne sont pas symétriques. Le complémentaire des 3 disques dessine 3 domaines fondamentaux d'orbite disjointe. L'un contient l'infini et est bordé par 5 arcs de cercles. L'autre est bordé par 4 arcs et le dernier par 3. On peut voir l'ensemble limite et le pavage par les domaines fondamentaux sur l'image ci-contre. Plus de détails sur l'article suivant sur Images des Mathématiques.
Quelques groupes fuchsiens
- Le groupe modulaire $\Gamma=\mathrm{PSL}_2(\mathbb{Z})$ a pour ensemble limite $\R\cup\{\infty\}\subset\widehat{\C}$.
Il possède des éléments de torsion d'ordre 2 et d'ordre 3. Il préserve le demi-plan supérieur et y a pour domaine fondamental par exemple $D$ défini par $\Im(z)>0$, $\Re(z)\in]-1/2,1/2[$, $|z|>1$. Pour la métrique hyperbolique sur ce demi-plan, $D$ est de volume fini. Un domaine fondamental symétrique existe pour le demi-plan inférieur. Un sous-groupe sans torsion est par exemple obtenu en prenant les matrices congrues à l'identité modulo 2, c'est un sous-groupe d'indice 6, et le quotient est conformément équivalent à la sphère de Riemann moins 3 points.
- Un groupe co-compact.
C'est le quotient sur $\mathbb{H}^2$ qui va être compact, et non pas sur $\mathbb{H}^3$. On prend un octogone régulier dans le plan hyperbolique. L'angle au sommet dépend de façon monotone de sa taille et peut prendre toutes les valeurs entre 0 et l'angle d'un octogone régulier euclidien (exclu). On peut en particulier le choisir de façon à valoir 1/8e de tour. On recolle ensuite les bords comme sur le dessin ci-contre. Les huits sommets sont alors identifiés. Sur le dessin, est indiqué dans quel ordre on les parcoure quand on tourne dans le sens trigonométrique autour du point obtenu. Le quotient est une 2-variété hyperbolique, surface de genre 2. Le sous-groupe engendré par les recollements est sans torsion et possède l'octogone pour domaine fondamental. L'ensemble limite est le bord du plan hyperbolique, i.e. le bord du cercle bleu dans l'image ci-contre.
- Un groupe Fuchsien dit de type II.
C'est à dire dont l'ensemble limite n'est pas tout le cercle, donc est un Cantor. C'est aussi un groupe de Schottky. Nous avons choisi le groupe engendré par $z\mapsto\frac{z+a}{1+az}$ et $z\mapsto\frac{z+ia}{1-iaz}$ avec $a=4/5$. Nous avons fait figurer le pavage par le domaine fondamental de Dirichlet de l'origine relativement à la structure hyperbolique du disque unité. Sa réunion avec son reflet hors du disque donne un pavage de l'ensemble de discontinuité de l'action sur la sphère de Riemann.
Des groupes quasifuchsiens
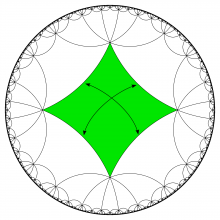
Informellement, les groupes quasifuchsiens sont les déformations des groupes fuchsiens chez les groupes kleiniens. Dans l'exemple ci-dessous nous avons dessiné l'ensemble limite d'une déformation du groupe Fuchsien associé à l'orbifold du tore carré avec un point orbifold d'ordre 2. Sur l'image de droite, on a figuré en vert un domaine fondamental particulier pour l'action sur l'ensemble de discontinuité, ainsi que le pavage induit et en rouge les points fixes des éléments de torsion. La figure du centre illustre le groupe Fuchsien qui a été déformé. On y voit un pavage du disque de Poincaré par un domaine fondamental, un carré hyperbolique à coins d'angle 1/8e de tour. Sur cette image, le points de torsion sont exactement les coins des carrés. Ce groupe a deux générateurs, qui recollent les côtés opposés du domaine fondamental.
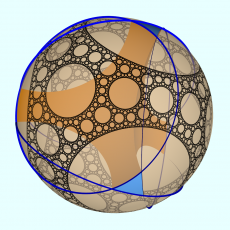
Un groupe de Schottky
À droite, l'ensemble limite d'un groupe de Schottky. C'est une poussière de Cantor. Le groupe a deux générateurs. Il y 4 disques disjoints tels que les deux générateurs envoient l'extérieur d'un disque sur l'intérieur d'un autre, comme sur la figure de gauche. Les zones blanches et jaunes sont un pavage par un domaine fondamental (le complément de tous les disques).
Un domaine fondamental dans H3 est donné par le demi-espace moins 4 demi-sphères de grand-cercles basés sur ces disques. Ces demi-sphères sont totalement géodésique, i.e. ce sont des plans hyperboliques. Sur l'image en 3D, l'espace hyperbolique est le demi-espace délimité par un plan horizontal et situé en dessous, le domaine fondamental mentionné ci-dessus est la région pleine possédant une face brune, contenue dans le plan horizontal (l'infini). Les images des demi-sphères par le groupe apparaissent également, alternativement en blanc et en brun, en fonction de la parité de la longueur du mot le plus court dans le groupe libre qui envoie sur telle out telle sphère l'une des 4 sphères de base.
Espace dodécaédral de Seifert Weber
Voir l'article Seifer Weber space sur Wikipedia, court et informatif (au 6 mai 2014). J'ai ici dessiné un domaine fondamental pour l'action du groupe Kleinien dans le modèle $\mathbb{H}^3$ de la boule de Poincaré, domaine qui est le dodécaèdre utilisé dans sa définition. L'angle entre deux faces adjacentes est d'un 1/5 de tour. Le groupe n'a pas de torsion.
$PSL_2(\mathbb{Z}[i])$
Analogue de $PSL_2(\mathbb{Z})$. L'ensemble limite est toute la sphère de Riemann. On a ici représenté un domaine fondamental dans le modèle demi-espace de Poincaré. C'est le demi-cylindre infini à base carrée de côté 1 privé de la sphère de rayon 1, tout deux centrés à l'origine. Le damier dessiné sur le plan à l'infini est un domaine fondamental pour l'action du sous-groupe des translations. le domaine doit encore être coupé en deux.
Un Tapis de Sierpiski
Dans le modèle de $\mathbb{H}^3$ par une boule B, un tétraèdre régulier et centré est le complémentaire dans B de 4 boules euclidiennes de même rayon et de bord orthogonal à celui de B. Plus on éloigne les sommets, plus ces boules diminuent de diamètre, jusqu'au moment où les sommets se retrouvent à l'infini de $\mathbb{H}^3$, c'est à dire sur le bord de B. L'angle entre les faces vaut alors $\pi/3$. Si on continue à diminuer le diamètre des boules les sommets n'existent plus mais on peut continuer à considérer leur complémentaire dans B et appeler cela un tétraèdre. Il possède un bord idéal (le bord de B privé des 4 boules), avec 4 composantes. L'angle entre les faces diminue jusqu'au moment ou il s'annule, après quoi les faces ne s'intersectent même plus, et les bord idéal devient connexe. On peut étudier pour quelles valeurs du diamètre le groupe de réflexion engendré par les 4 sphères est un groupe Kleinien, c'est un problème intéressant que nous n'aborderons pas ici. Il existe une unique valeur du diamètre tel que l'angle entre 2 plans vaut $2\pi/7$, le tétraèdre correspondant a du bord idéal. Le groupe de réflexion engendré est Kleinien et le tétraèdre est presque un domaine fondamental pour l'action dans $\mathbb{H^3}$: c'est l'union de 24 morceaux, images d'un même domaine fondamental par le groupe de réflexion préservant le tétraèdre. Dans les images ci-dessous, nous illustrions son ensemble limite, un pavage par un domaine fondamental dans l'ensemble de discontinuité, et le tétraèdre à l'intérieur. Cet ensemble limite est un exemple de Tapis de Sierpinski. Il est remarquable que les composantes de l'ensemble de discontinuité soient de vrais disques, et que le fixateur de chacun par le groupe soit exactement le groupe de réflexion associé au triangle 2-3-7.