Interface with FFT libraries
In Montjoie, you can compute Fast Fourier Transforms by using several libraries. Currently, we have interfaced three libraries, MKL (enabled if you set USE_MKL := YES in the makefile), Gsl (enabled if you set USE_GSL := YES) and Fftw (enabled if you set USE_FFTW := YES), we propose also a basic implementation (using Cooley-Turkey algorithm), so that you can run Montjoie without linking these libraries. This basic implementation is working only if N is a power of 2. We have compared the efficiency of different libraries in the table below (computational time for backward and forward fft for a 3-D array of size N x N x N).
| N = 128 | N = 256 | N = 512 | |
| Manual | 0.28s | 2.81s | 25.1s |
| Gsl | 0.259s | 3.44s | 41.5 |
| Fftw | 0.088s | 0.858s | 11.2s |
| MKL | 0.05s | 0.494s | 5.52s |
For this case and the architecture used, MKL seems the more efficient.
Basic Use
The interface is implemented for real and complex numbers. The selection of the default library to use is automatically done : if you have compiled Montjoie with Mkl it will use the Fft proposed by MKL, otherwise if you have compiled it with Fftw, it will use Fftw library, otherwise if you have compiled it with Gsl, it will use Gsl library. If none of these libraries have been linked in the Makefile, it will use the default implementation (only working if N is a power of 2). For real numbers, the result of the forward transform is a complex vector of size N/2+1 (the other N/2+1 components are not stored since they are the conjugate of the first ones).
// you declare the Montjoie class to perform fft FftInterface<complex<double> > fft; // initialisation to perform backward and/or forward fft for vectors of size N int N = 32; fft.Init(N); // then you replace vectors with their discrete Fourier transforms Vector<complex<double> > y(N); y.FillRand(); // forward fft fft.ApplyForward(y); // backward fft fft.ApplyInverse(y); // class to perform fft for real numbers FftRealInterface fft_real; // initialisation fft_real.Init(N); Vector<double> u(N); // the forward transform is a complex vector of size N/2+1 Vector<complex<double> > uhat(N/2+1); fft_real.ApplyForward(u, uhat); // and for inverse transform, the result is a real vector // and the input vector is complex fft_real.ApplyInverse(uhat, u);
Methods of FftInterface
| SelectFftAlgorithm | selects another FFT library to use |
| GetNbPoints | returns the number of points |
| GetMemorySize | returns the memory used by the object |
| SetNbThreads | returns the number of threads for fftw |
| Init | initialization for vectors of size n |
| ApplyForward | overwrites vector with its forward discrete Fourier transform |
| ApplyInverse | overwrites vector with its backward discrete Fourier transform |
| ApplyForwardPoint | computes forward Fourier transform of a vector for a single value of k. |
| ApplyInversePoint | computes backward discrete Fourier transform of a vector for a single value of k. |
| GetCoefficient | returns the complex phase for a single pair of indices |
| GetCosSinAlpha | retrieves the cosine and sine of the angle associated with fft |
Methods of FftRealInterface
| GetNbPoints | returns the number of points |
| GetMemorySize | returns the memory used by the object |
| SetNbThreads | returns the number of threads for fftw |
| Init | initialization for vectors of size n |
| ApplyForward | computes Fourier transform of a real vector |
| ApplyInverse | computes inverse Fourier transform of a complex vector |
SelectFftAlgorithm
Syntax
void SelectFftAlgorithm(int type) const;
This method selects the FFT library to use. You have the choice between MANUAL, FFT_MKL, FFTW and FFT_GSL. The manual choice is the basic algorithm, it should be avoided, while other choices are associated with Mkl, Fftw and Gsl implementations of FFTs. Usually this method should not be called since the fastest available library is selected in the default constructor.
Example :
int n = 14; FftInterface<complex<double> > fft; // prior to any use, you can ask to use another library (different from the default one which is the fastest) fft.SelectFftAlgorithm(fft.FFTW); // then you can use the object fft.Init(n); Vector<double> x(n); fft.ApplyForward(x);
Location :
GetNbPoints
Syntax
int GetNbPoints() const;
This method returns the number of points for which the structure is ready to compute 1-D fft.
Example :
int n = 14; FftInterface<complex<double> > fft; fft.Init(n); // GetNbPoints() should return n cout << "Number of points = " << fft.GetNbPoints() << endl;
Location :
GetMemorySize
Syntax
size_t GetMemorySize() const;
This method returns the memory used to store the object in bytes.
Example :
int n = 14; FftInterface<complex<double> > fft; fft.Init(n); // memory used to store fft cout << "Memory used to store fft = " << fft.GetMemorySize() << " bytes " << endl;
Location :
SetNbThreads
Syntax
void SetNbThreads(int n);
This method sets the number of threads to use. It is used only with FFTW interface, and should be called before Init. By default (if this method is not called), the number of threads is set to omp_get_max_threads().
Example :
int n = 32; FftInterface<complex<double> > fft; // if you want to limit the number of threads with fftw fft.SetNbThreads(8); // then you call Init fft.Init(n);
Location :
Init
Syntax
void Init(int N); void Init(int nx, int ny); void Init(int nx, int ny, int nz);
This method prepares the computation of fft for vectors of size N. This step is mandatory, and you need to call it again if you want to perform a discrete Fourier transform of a vector with a different size. You can also initialize the computation of 2-D FFTs and 3-D FFTs.
Example :
int n = 32;
FftInterface<complex<double> > fft;
fft.Init(n);
Vector<complex<double> > x(n);
fft.ApplyForward(x);
// for 2-D FFTs
int nx = 32, ny = 60, nz = 120;
FftInterface<complex<double> > fft2d;
// Init is called with two integers for 2-D ffts
fft2d.Init(nx, ny);
// the vector contains all the values u_{i, j}
x.Reallocate(nx*ny);
// x is replaced by its discrete Fourier transform
fft.ApplyForward(x);
// for 3-D FFTs
FftInterface<complex<double> > fft3d;
// Init is called with three integes
fft2d.Init(nx, ny, nz);
// the vector contains all the values u_{i, j, k}
x.Reallocate(nx*ny*nz);
// x is replaced by its discrete Fourier transform
fft.ApplyForward(x);
Location :
ApplyForward
Syntax
void ApplyForward(Vector<T> & u);
This method overwrites a vector by its discrete Fourier transform, in 1-D:
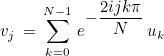
For 2-D FFTs, the following formula is used:
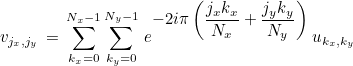
The values um, n are stored in a 1-D vector as u(m*Ny+n). For 3-D FFTs, the following formula is used:
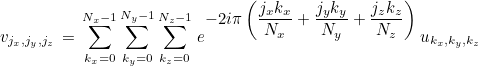
The values um, n, p are stored in a 1-D vector as u(N_z*(m*Ny + n) + p).
Example :
// usually it is more efficient to choose a number with factors 2, 3, 5 and 7
int n = 210;
FftInterface<complex<double> > fft;
// 1-D FFTs
fft.Init(n);
Vector<complex<double> > u(n);
Vector<double> x;
Linspace(-5.0, 5.0, n, x);
for (int i = 0; i < n; i++)
u(i) = exp(-5.0*x(i)*x(i));
// u is replaced by its discrete Fourier transform
fft.ApplyForward(u);
// 2-D FFTs
int nx = 32, ny = 80, nz = 20;
Vector<double> y, z;
Linspace(-5.0, 5.0, nx, x);
Linspace(-4.0, 4.0, ny, y);
Linspace(-2.0, 3.0, nz, z);
u.Reallocate(nx*ny);
for (int i = 0; i < nx; i++)
for (int j = 0; j < ny; j++)
u(i*ny + j) = exp(-5.0*(x(i)*x(i) + y(j)*y(j)));
// Init must be called with two integers for 2-D ffts
fft.Init(nx, ny);
// u is replaced by its discrete Fourier transform
fft.ApplyForward(u);
// 3-D FFTs
int nx = 32, ny = 80, nz = 20;
u.Reallocate(nx*ny*nz);
for (int i = 0; i < nx; i++)
for (int j = 0; j < ny; j++)
for (int j = 0; j < nz; j++)
u(i*ny + j) = exp(-5.0*(x(i)*x(i) + y(j)*y(j) + z(j)*z(j)));
// Init must be called with three integers for 3-D ffts
fft.Init(nx, ny, nz);
// u is replaced by its discrete Fourier transform
fft.ApplyForward(u);
Location :
ApplyInverse
Syntax
void ApplyInverse(Vector<T> & x);
This method overwrites a vector by its discrete backward Fourier transform :
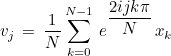
For 2-D FFTs, the following formula is used:
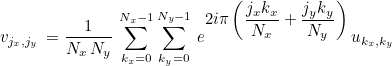
The values um, n are stored in a 1-D vector as u(m*Ny+n). For 3-D FFTs, the following formula is used:
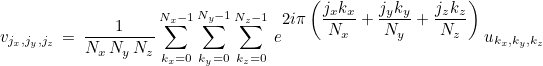
The values um, n, p are stored in a 1-D vector as u(N_z*(m*Ny + n) + p).
Example :
// usually it is more efficient to choose a number with factors 2, 3, 5 and 7
int n = 210;
FftInterface<complex<double> > fft;
// 1-D FFTs
fft.Init(n);
Vector<complex<double> > u(n);
Vector<double> x;
Linspace(-5.0, 5.0, n, x);
for (int i = 0; i < n; i++)
u(i) = exp(-5.0*x(i)*x(i));
// u is replaced by its discrete backward Fourier transform
fft.ApplyInverse(u);
// 2-D FFTs
int nx = 32, ny = 80, nz = 20;
Vector<double> y, z;
Linspace(-5.0, 5.0, nx, x);
Linspace(-4.0, 4.0, ny, y);
Linspace(-2.0, 3.0, nz, z);
u.Reallocate(nx*ny);
for (int i = 0; i < nx; i++)
for (int j = 0; j < ny; j++)
u(i*ny + j) = exp(-5.0*(x(i)*x(i) + y(j)*y(j)));
// Init must be called with two integers for 2-D ffts
fft.Init(nx, ny);
// u is replaced by its discrete backward Fourier transform
fft.ApplyInverse(u);
// 3-D FFTs
int nx = 32, ny = 80, nz = 20;
u.Reallocate(nx*ny*nz);
for (int i = 0; i < nx; i++)
for (int j = 0; j < ny; j++)
for (int j = 0; j < nz; j++)
u(i*ny + j) = exp(-5.0*(x(i)*x(i) + y(j)*y(j) + z(j)*z(j)));
// Init must be called with three integers for 3-D ffts
fft.Init(nx, ny, nz);
// u is replaced by its discrete backward Fourier transform
fft.ApplyInverse(u);
Location :
ApplyForwardPoint
Syntax
void ApplyForwardPoint(int j, Vector<T>& u, T& v); void ApplyForwardPoint(int jx, int jy, Vector<T>& u, T& v); void ApplyForwardPoint(int jx, int jy, int jz, Vector<T>& u, T& v);
This method computes a component of forward Fourier transform (j is given) :
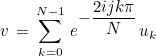
Of course, for this computation, we are using the naive algorithm, since faster algorithms are obtained only when all the components of Fourier transform are needed. The two last syntaxes are dealing with 2-D and 3-D discrete Fourier transforms.
Example :
int n = 14; FftInterface<complex<double> > fft; fft.Init(n); Vector<complex<double> > y(n); y.FillRand(); // we compute discrete forward Fourier transform for a given value of j int j = 3; complex<double> v; fft.ApplyForwardPoint(j, y, v);
Location :
ApplyInversePoint
Syntax
void ApplyInversePoint(int j, Vector<T>& u, T& v); void ApplyInversePoint(int jx, int jy, Vector<T>& u, T& v); void ApplyInversePoint(int jx, int jy, int jz, Vector<T>& u, T& v);
This method computes a component of inverse Fourier transform (j is given) :
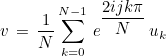
Of course, for this computation, we are using the naive algorithm, since faster algorithms are obtained only when all the components of Fourier transform are needed. The two last syntaxes are dealing with 2-D and 3-D discrete Fourier transforms.
Example :
int n = 14; FftInterface<complex<double> > fft; fft.Init(n); Vector<complex<double> > y(n); y.FillRand(); // we compute discrete backward Fourier transform for a given value of j int j = 3; complex<double> v; fft.ApplyInversePoint(j, y, v);
Location :
GetCoefficient
Syntax
Complex_wp GetCoefficient(int j, int k) Complex_wp GetCoefficient(int jx, int jy, int kx, int ky) Complex_wp GetCoefficient(int jx, int jy, int jz, int kx, int ky, int kz)
This method computes a coefficient involved in inverse Fourier transform (j and k are given) :
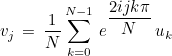
We see that we have
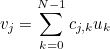
where the coefficients cj, k are given as:
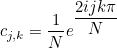
The method GetCoefficient returns this coefficient cj, k. Other syntaxes returns coefficients for 2-D and 3-D Fourier transforms.
Example :
int n = 14;
FftInterface<complex<double> > fft;
fft.Init(n);
// a single coefficient c_{2, 3}
// c_{j, k} are coefficients such that v_j = \sum c_{j, k} u_k
// is the inverse FFT
Complex_wp coef = fft.GetCoefficient(2, 3);
GetCosSinAlpha
Syntax
void GetCosSinAlpha(int n, Real_wp& cos_alpha, Real_wp& sin_alpha);
This method sets cos_alpha and sin_alpha to the cosine and sine of the following angle:
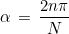
Example :
int n = 14; FftInterface<Complex_wp> fft; fft.Init(n); // the cosine and sine of 2 pi n /N can be retrieved : Real_wp cos_alpha, sin_alpha; int n = 3; fft.GetCosSinAlpha(n, cos_alpha, sin_alpha);
Location :
Init
Syntax
void Init(int n);
This method prepares the computation of forward/backward FFT of size n. It is mandatory to call it. Only 1-D FFTs are currently implemented for the real interface.
Example :
int n = 14; FftRealInterface fft_real; fft_real.Init(n); Vector<double> x(n); Vector<complex<double> > y(n/2+1); fft_real.ApplyForward(x, y);
Location :
ApplyForward
Syntax
void ApplyForward(const Vector<double> & x, Vector<complex<double> > &y);
This method computes the discrete Fourier transform of a real vector
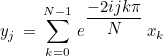
Since x is real, the last N/2 components of y are the conjugates of the first N/2 components (in a reverse order), therefore y is a complex vector of size N/2 + 1. Only the first N/2+1 components are effectively stored.
Example :
int n = 14; FftRealInterface fft_real; fft_real.Init(n); Vector<double> x(n); Vector<complex<double> > y(n/2+1); fft_real.ApplyForward(x, y);
Location :
ApplyInverse
Syntax
void ApplyInverse(Vector<complex<double>> & x, Vector<double> & y);
This method computes the inverse Fourier transform of a complex vector such that the result is a real vector
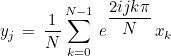
The complex vector is assumed to have its last N/2 components as conjugates of the first N/2 components (in a reverse order), such that the inverse Fourier transform is real. Only the first N/2+1 components of the complex vector are stored and given in this method.
Example :
// example of computation of the derivative of a function with fft Real_wp a = -10.0, b = 10.0; int N = 200; VectReal_wp t; Linspace(a, b, N, t); VectReal_wp f(N), df(N); VectComplex_wp fchap(N/2+1); // evaluation of the original function for (int i = 0; i < N; i++) f(i) = exp(-t(i)*t(i))*cos(2.0*pi_wp*t(i)); // omega_i for each frequency VectReal_wp omega(N/2+1); for (int i = 0; i < N/2+1; i++) omega(i) = 2.0*pi_wp*Real_wp(i)/(b-a); // initialisation of the fft FftRealInterface fft; fft.Init(N); // Forward transform, fchap is complex fft.ApplyForward(f, fchap); // multiplication by i omega to get the Fourier transform of derivative of f for (int i = 0; i < N/2+1; i++) fchap(i) *= Iwp*omega(i); // inverse Fourier transform to obtain the derivative of f fft.ApplyInverse(fchap, df);