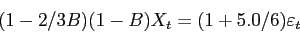Estimation des parametres par SAS

1. Ecrire le modèle MA(2) 1.4.2 sous forme canonique (telle que les racines du polynôme $\Theta(B)$ ont modules strictement superieures à 1. Estimer les paramètres avec la méthode estimate du processus arima

   Corrigé Le polynôme $1+0.4z-0.8z^2$ possède deux racines réelle $z_1=1.396>1$ et $z_2=-0.896$, la deuxième racine a une module strictement inférieure à 1. (On peut vérifier sous matlab avec la commande : roots([-0.8 0.4 1]) ) donc le processus MA(2) défini par $\varepsilon _t + 0.4 \varepsilon _{t-1} -0.8 \varepsilon _{t-2}$ n'est pas sous sa forme canonique. Après calcul (voir exercice), on peut montrer que ce processus possède les mêmes statistiques que le processus suivant
   

   $$\bgroup\color{blue} w_t = u_t + 0.179u_{t-1} - 0.642u_{t-2}   u_t \sim N(0,0.05) \egroup$$
   
   
   Ici $0.05 = \frac{0.2^2}{0.896 ^2}$

    
   title1 'Simulated MA(2) Series';
     data a;
       e1 = 0; e2 = 0;
       do i = -50 to 10000;
          e = 0.2*rannor( 3255 );
          x = e + 0.4 * e1 - .8 * e2;
          if i > 0 then output;
          e2 = e1;
          e1 = e;
          end;
     run;
   
   symbol interpol=join color=black value=none;
   proc gplot data=a;
      plot x*i;
   run;
   
   proc arima data=a;
     identify var=x;
     run;
     estimate q=2; /* estimation MA(2) */
     run;
   quit;
   

   
   le procedure arima estime que le modele est

    
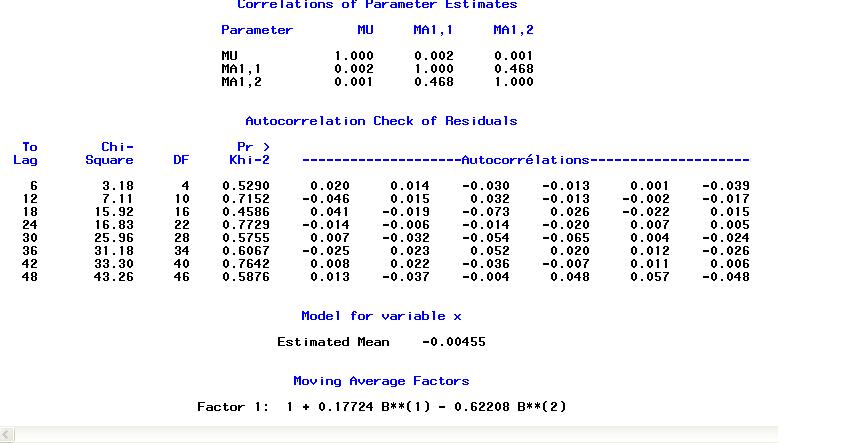
   1 + 0.17724 B**(1) - 0.62208 B(2)
   

   assez proche des valeurs théoriques.
2. Estimer les paramètres du modèle 2.1.3.

   Corrigé

    
   title1 'Simulated AR(1)';
   data a;
       u1 = 0;
       do i = -50 to 500;
          a = rannor( 32565 );
          u = 0.75*u1 + 0.2*a;
          if i > 0 then output;         
          u1 = u;
          end;
     run;
     symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   
   proc arima data=a;
       identify var=u; run;
      estimate p=1; run;
   quit;
   

   
   On voit bien la residu est un bruit blanc ce qui valide le modele AR(1)

3. Estimer les paramètres du modèle 2.1.6.

   Corrigé

    
   title1 'Simulated AR(2)';
   data a;
       u1 = 0; u2=0;
       do i = -50 to 1000;
          a = rannor( 32565 );
          u = (5.0/6)*u1 -(1.0/6)*u2 + 0.2*a;
          if i > 0 then output;         
          u2 = u1; u1 = u;         
       end;
     run;
   
   symbol1 interpol=join color=black value=none;
   proc gplot data=a;
      plot u*i;
   run;
   
   proc arima data=a;
      identify var = u; run;
      estimate p=2; run;
   quit;
   

   
   le procédure arima estime que le modèle ar(2) est

    
   1 - 0.75634 B**(1) + 0.13492 B**(2)
   

   le vrai modèle est $1-0.83 B + 0.16 B^2$.
4. . On considère maintenant le processus ARIMA(1,1,1) suivant
   
   $$\bgroup\color{blue} (1-\frac23B)(1-B) X_t = \varepsilon _t ... ...on _{t-1}   \mbox{o\\lq u}  \varepsilon \sim N(0,0.2^2) \egroup$$
   
   
   1. Est-ce que le modèle est sous la forme canonique ?

      Corrigé Oui, pour faciler la simulation on peut écrire le processus par
      

      $$X_t = \frac53 X_{t-1}-\frac23X_{t-2}+\varepsilon _t + \frac56 \varepsilon _{t-1}$$
      
      

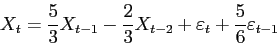
   2. Simuler ce processus.

      Corrigé

       
      title1 'Simulated ARIMA(1,1,1)';
      data a;
          u1=0; u2=0 ; a1 = 0;
          do i = -50 to 10000;
             a = 0.2*rannor(1);
             u = (5.0/3)*u1 - (2.0/3)*u2 + a + (5.0/6)*a1;
             if i > 0 then output;         
             u2 = u1; u1 = u; a1 = a;
          end;
        run;
      
      symbol1 interpol=join color=black value=none;
      proc gplot data=a;
         plot u*i;
      run;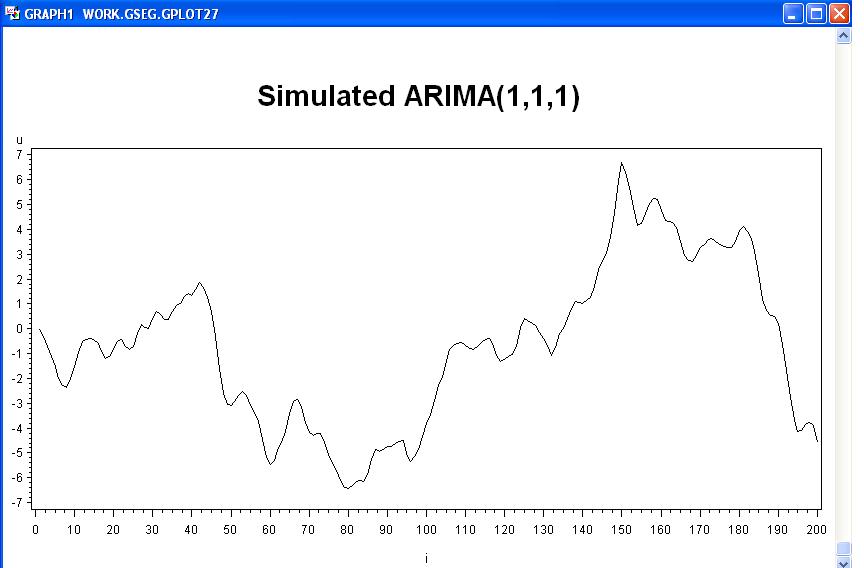
      

      
   3. On suppose que les ordre (p,d,q) = (1,1,1) sont connus, identifier et estimer les parametres de ce processus. Expliquer chacun des resultats.

      Corrigé (Suite)

       
      proc arima data=a;
         identify var=u;run;
         identify var=u(1); run;
         estimate p=1 q=1; run;
      quit;
      

      
      le procédure arima estime que le modèle arima(1,1,1) est

       
      AR(1): 1 - 0.61058 B**(1) et MA(1) : 1+0.85056 B*(1)
      

      le vrai modèle est
      
      $$(1-2/3B)(1-B) X_t = (1 + 5.0/6)\varepsilon _t$$