Identification avec scan esacf et minic

1. Stationnarité d'un BBG par les tests de Augumented Dicker-Fuller.
   1. Simuler le processus 2.1.1 identify le avec option stationarity(DICKEY);

      Corrigé On remarque dans la colonne Pr>F il y que des probabilités très faible donc les modèles M1, M2, M3 sont tous invraisemblable, c'est à dire le processus d'admet pas de racine unité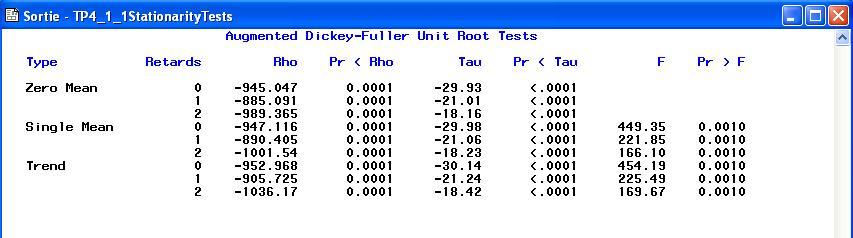

      
   2. utiliser la méthode suivante pour identifier le processus précédent, expliquer les resultats

       
      identify var=u nlag=12 minic scan esacf;run;+
      

      Corrigé la méthode minic propose BIC(0,0), c'est à dire ARMA(0,0), le tableau suivant donne le résumé de ces trois méthodes:

      
      On voit bien que le modèle ARMA(0,0) modélise bien ce processus.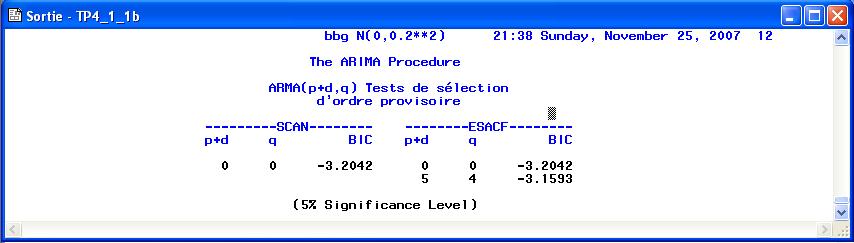
2. Même question pour le processus AR(1) simulé par 2.1.3

    
   title1 'Simulated AR(1)';
   data a;
       u1 = 0;
       do i = -50 to 10000;
          a = rannor( 32565 );
          u = 0.75*u1 + 0.2*a;
          if i > 0 then output;         u1 = u;
          end;
     run;
   proc arima data=a;
     identify var=u stationarity=(DICKEY); run;
     /* on voit c est un AR(1) par correlogramme partiel
        et ADF montre qu'il a pas de racine unite
        residu n est pas bruit blanc mais le processus semble stationnaire
     */
     identify var=u minic scan esacf; run;
     /* il est interessant de constater que
        avec nombre tirage = 500, on trouve plusieurs modeles possibles,
        mais avec 1000 tirages, les 3 m\'ethodes minic, scan et esacf donnent la meme
        modele : ARMA(1,0)
     */
   quit;